
 已知抛物线y=x2-2mx+m2+m-1(m是常数)的顶点为P,直线l:y=x-1.
已知抛物线y=x2-2mx+m2+m-1(m是常数)的顶点为P,直线l:y=x-1.分析 (1)利用配方法得到y=(x-m)2+m-1,点P(m,m-1),然后根据一次函数图象上点的坐标特征判断点P在直线l上;
(2)当m=-3时,抛物线解析式为y=x2+6x+5,根据抛物线与x轴的交点问题求出A(-5,0),易得C(0,5),通过解方程组$\left\{\begin{array}{l}{y={x}^{2}+6x+5}\\{y=x-1}\end{array}\right.$得P(-3,-4),Q(-2,-3),作ME⊥y轴于E,PF⊥x轴于F,QG⊥x轴于G,如图,证明Rt△CME∽Rt△PAF,利用相似得$\frac{ME}{AF}$=$\frac{CE}{PF}$,设M(x,x2+6x+5),则$\frac{-x}{2}$=$\frac{-{x}^{2}-6x}{4}$,解得x1=0(舍去),x2=-4,于是得到点M的坐标为(-4,-3);
(3)通过解方程组$\left\{\begin{array}{l}{y={x}^{2}-2mx+{m}^{2}+m-1}\\{y=x-1}\end{array}\right.$得P(m,m-1),Q(m+1,m),利用两点间的距离公式得到PQ2=2,OQ2=2m2+2m+1,OP2=2m2-2m+1,然后分类讨论:当PQ=OQ时,2m2+2m+1=2;当PQ=OP时,2m2-2m+1=2;当OP=OQ时,2m2+2m+1=2m2-2m+1,再分别解关于m的方程求出m即可.
解答 (1)证明:∵y=x2-2mx+m2+m-1=(x-m)2+m-1,
∴点P的坐标为(m,m-1),
∵当x=m时,y=x-1=m-1,
∴点P在直线l上;
(2)解:当m=-3时,抛物线解析式为y=x2+6x+5,
当y=0时,x2+6x+5=0,解得x1=-1,x2=-5,则A(-5,0),
当x=0时,y=x2+6x+5=5,则C(0,5),
可得解方程组$\left\{\begin{array}{l}{y={x}^{2}+6x+5}\\{y=x-1}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=-3}\\{y=-4}\end{array}\right.$或$\left\{\begin{array}{l}{x=-2}\\{y=-3}\end{array}\right.$,
则P(-3,-4),Q(-2,-3),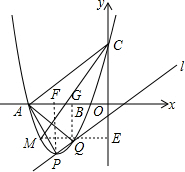 作ME⊥y轴于E,PF⊥x轴于F,QG⊥x轴于G,如图,
作ME⊥y轴于E,PF⊥x轴于F,QG⊥x轴于G,如图,
∵OA=OC=5,
∴△OAC为等腰直角三角形,
∴∠ACO=45°,
∴∠MCE=45°-∠ACM,
∵QG=3,OG=2,
∴AG=OA-OG=3=QG,
∴△AQG为等腰直角三角形,
∴∠QAG=45°,
∵∠APF=90°-∠PAF=90°-(∠PAQ+45°)=45°-∠PAQ,
∵∠ACM=∠PAQ,
∴∠APF=∠MCE,
∴Rt△CME∽Rt△PAF,
∴$\frac{ME}{AF}$=$\frac{CE}{PF}$,
设M(x,x2+6x+5),
∴ME=-x,CE=5-(x2+6x+5)=-x2-6x,
∴$\frac{-x}{2}$=$\frac{-{x}^{2}-6x}{4}$,
整理得x2+4x=0,解得x1=0(舍去),x2=-4,
∴点M的坐标为(-4,-3);
(3)解:解方程组$\left\{\begin{array}{l}{y={x}^{2}-2mx+{m}^{2}+m-1}\\{y=x-1}\end{array}\right.$得$\left\{\begin{array}{l}{x=m}\\{y=m-1}\end{array}\right.$或$\left\{\begin{array}{l}{x=m+1}\\{y=m}\end{array}\right.$,则P(m,m-1),Q(m+1,m),
∴PQ2=(m+1-m)2+(m-m+1)2=2,OQ2=(m+1)2+m2=2m2+2m+1,OP2=m2+(m-1)2=2m2-2m+1,
当PQ=OQ时,2m2+2m+1=2,解得m1=$\frac{-1+\sqrt{3}}{2}$,m2=$\frac{-1-\sqrt{3}}{2}$;
当PQ=OP时,2m2-2m+1=2,解得m1=$\frac{1+\sqrt{3}}{2}$,m2=$\frac{1-\sqrt{3}}{2}$;
当OP=OQ时,2m2+2m+1=2m2-2m+1,解得m=0,
综上所述,m的值为$\frac{-1+\sqrt{3}}{2}$,$\frac{-1-\sqrt{3}}{2}$,$\frac{1+\sqrt{3}}{2}$,$\frac{1-\sqrt{3}}{2}$,0.
点评 本题考查了二次函数的综合题:熟练掌握二次函数图象和一次函数图象上点的坐标特征、二次函数的性质,会求抛物线与直线的交点坐标;理解坐标与图形性质,会利用两点间的距离公式计算线段的长;会运用相似比计算线段的长;能运用分类讨论的思想解决数学问题.


科目:初中数学 来源: 题型:填空题
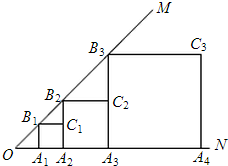 如图,∠MON=45°,OA1=1,作正方形A1B1C1A2,周长记作L1;再作第二个正方形A2B2C2A3,周长记作L2;继续作第三个正方形A3B3C3A4,周长记作L3;点A1、A2、A3、A4…在射线ON上,点B1、B2、B3、B4…在射线OM上,…依此类推,则第n个正方形的周长Ln=2n+1.
如图,∠MON=45°,OA1=1,作正方形A1B1C1A2,周长记作L1;再作第二个正方形A2B2C2A3,周长记作L2;继续作第三个正方形A3B3C3A4,周长记作L3;点A1、A2、A3、A4…在射线ON上,点B1、B2、B3、B4…在射线OM上,…依此类推,则第n个正方形的周长Ln=2n+1.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{5}$ | B. | -$\frac{1}{5}$ | C. | -1 | D. | -3 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在正方形ABCD中,AB=4,点E为CD上一动点,AE交BD于点F,过点F作FH⊥AE,交BC于H,过H作GH⊥BD于点G,下列结论:①AF=FH,②∠HAE=45°,③BD=$\frac{3}{2}$FG,④△CEH的周长为定值.其中正确的是①②④(写正确结论的序号).
如图,在正方形ABCD中,AB=4,点E为CD上一动点,AE交BD于点F,过点F作FH⊥AE,交BC于H,过H作GH⊥BD于点G,下列结论:①AF=FH,②∠HAE=45°,③BD=$\frac{3}{2}$FG,④△CEH的周长为定值.其中正确的是①②④(写正确结论的序号).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | m<3 | B. | m>3 | C. | m<0 | D. | m>0 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 图象中所反映的过程是:小强从家跑步去体育场,在那里锻炼了一阵后,又去早餐店吃早餐,然后散步走回家,其中x表示时间,y表示小强离家的距离.图象提供的信息,有以下四个说法:
图象中所反映的过程是:小强从家跑步去体育场,在那里锻炼了一阵后,又去早餐店吃早餐,然后散步走回家,其中x表示时间,y表示小强离家的距离.图象提供的信息,有以下四个说法:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 年 | 上半年盈利 | 下半年盈利 | 算式 | 合计 |
| 第一年 | 1.2 | 0.8 | 1.2+0.8 | |
| 第二年 | -0.6 | -0.7 | (-0.6)+(-0.7) | |
| 第三年 | -0.5 | 0.5 | (-0.5)+0.5 | |
| 第四年 | 0.9 | -0.1 | 0.9+(-0.1) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com