练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    7．已知在卡乐芙超市内购物总金额超过190元时，购物总金额有打八折的优惠，安妮带200元到卡乐芙超市买棒棒糖．若棒棒糖每根9元，则她最多可买多少根棒棒糖（　　）
    A．22B．23C．27D．28

    分析 设买x根棒棒糖，根据题意列出不等式，解不等式即可．

    解答 解：设买x根棒棒糖，
    由题意得，9x×0.8≤200，
    解得，x≤$\frac{250}{9}$，
    ∴她最多可买27根棒棒糖，
    故选：C．

    点评 本题考查的是一元一次不等式的应用，根据题意正确列出不等式、并正确解出不等式是解题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

    5．在抛物线y=x2-6x+c上有三个点，A（-1，y1），B（2，y2），C（3+$\sqrt{2}$，y3）三点，则y1，y2，y3的大小关系是（　　）
    A．y1＞y2＞y3B．y1＜y2＜y3C．y1＞y3＞y2D．不确定

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

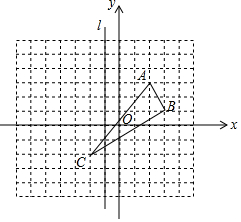    18．如图，已知△ABC的三个顶点分别为A（2，3），B（3，1），C（-2，-2），直线l是经过（-1，0）且垂直于x轴的一条直线．
    （1）请在图中作出△ABC关于直线l的轴对称图形△DEF（A，B，C的对应点分别是D，E，F），并直接写出D，E，F的坐标；
    （2）直接写出四边形ABED的面积；
    （3）若点M（-5，a-2）与点N（b，2a-1）关于直线l成轴对称，求a与b的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    15．先化简，再求值：（$\frac{1}{x-2}$+1）÷$\frac{x-1}{{x}^{2}-4}$，其中x=-sin30°．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    2．阅读下列材料：
    在数学课上，老师请同学们思考下列问题：如图1，我们把一个四边形ABCD的四边中点E、F、G、H依次连接起来得到的四边形EFGH是平行四边形吗？
    小敏在思考问题时，有如下思路：连接AC．
    点E、F分别是AB、BC的中点$\stackrel{三角形中位线定理}{→}$EF∥AC，EF=$\frac{1}{2}$AC；
    点H、G分别是AD、CD的中点$\stackrel{三角形中位线定理}{→}$HG∥AC，HG=$\frac{1}{2}$AC
    →EF∥HG，EF=HG→四边形EFGH是平行四边形．
    结合小敏的思路作答：
    （1）若只改变图1中四边形ABCD的形状（如图2），则四边形EFGH还是平行四边形吗？请说明理由；
    参考小敏思考问题的方法，解决以下问题：
    （2）如图2，在（1）的条件下，若连接AC，BD．
    ①当AC与BD满足什么关系时，四边形EFGH是菱形，写出结论并证明；
    ②当AC与BD满足什么条件时，四边形EFGH是矩形，直接写出结论．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    12．如图，某计算机中有、、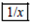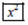三个按键，以下是这三个按键的功能．
    1．：将荧幕显示的数变成它的正平方根，例如：荧幕显示的数为49时，按下后会变成7．
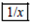    2．：将荧幕显示的数变成它的倒数，例如：荧幕显示的数为25时，按下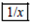后会变成0.04．
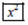    3．：将荧幕显示的数变成它的平方，例如：荧幕显示的数为6时，按下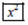后会变成36．
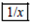    若荧幕显示的数为100时，小刘第一下按，第二下按，第三下按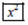，之后以、、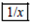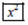的顺序轮流按，则当他按了第100下后荧幕显示的数是多少（　　）
    A．0.01B．0.1C．10D．100

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    19．某商场以180元/件的价格购进200件衬衫，当标价400元/件时无人购买，商场决定降价销售，连续降价两次后商场将这批衬衫以每件256元的价格全部售出，并且两次降价的百分率相同．
    （1）求该种衬衫每次降价的百分率．
    （2）商场为了使降价销售的总利润不少于28800元，则第一次降价后至少要售出多少件该种衬衫？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    16．已知方程组$\left\{\begin{array}{l}{ax+5y=15①}\\{4x-by=-2②}\end{array}\right.$，由于甲看错了方程（1）中的a得到方程组的解为$\left\{\begin{array}{l}{x=-3}\\{y=-1}\end{array}\right.$，乙看错了方程（2）中的b得到方程组的解为$\left\{\begin{array}{l}{x=5}\\{y=4}\end{array}\right.$，假如二人的计算过程没有错误，求原方程组正确的解．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

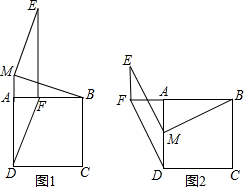    17．正方形ABCD的边长是5，点M是直线AD上一点，连接BM，将线段BM绕点M逆时针旋转90°得到线段ME，在直线AB上取点F，使AF=AM，且点F与点E在AD同侧，连接EF，DF．
    （1）如图?1，当点M在DA延长线上时，求证：△ADF≌△ABM；
    （2）如图2?，当点M在线段AD上时，四边形DFEM是否还是平行四边形，说明理由；
    （3）在（2）的条件下，线段AM与线段AD有什么数量关系时，四边形DFEM的面积最大？并求出这个面积的最大值．

    查看答案和解析>>

    同步练习册答案