
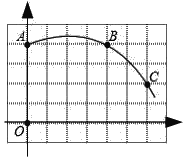
【题目】如图,网格纸中每个小正方形的边长为1,一段圆弧经过格点,点O为坐标原点.
(1)该图中弧所在圆的圆心D的坐标为 ;.
(2)根据(1)中的条件填空:
①圆D的半径= (结果保留根号);
②点(7,0)在圆D (填“上”、“内”或“外”);
③∠ADC的度数为 .
科目:初中数学 来源: 题型:
【题目】如图,AD是圆O的切线,切点为A,AB是圆O的弦。过点B作BC//AD,交圆O于点C,连接AC,过点C作CD//AB,交AD于点D。连接AO并延长交BC于点M,交过点C的直线于点P,且BCP=ACD。
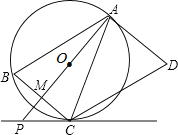
(1)判断直线PC与圆O的位置关系,并说明理由:
(2) 若AB=9,BC=6,求PC的长。
查看答案和解析>>
科目:初中数学 来源: 题型:
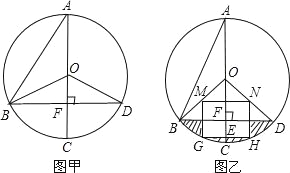
【题目】如图甲,已知在⊙O中,AB=![]() ,AC是⊙O的直径,AC⊥BD于F,∠A=30度.
,AC是⊙O的直径,AC⊥BD于F,∠A=30度.
(1)连接BC,CD,请你判定四边形OBCD是何种特殊的四边形?试说明理由;
(2)若用扇形OBD围成一个圆锥侧面,请求出这个圆锥的底面圆的半径;
(3)如图乙,若将“∠A=30°”改为“∠A=22.5°”,其余条件不变,以半径OB、OD的中点M、N为顶点作矩形MNGH,顶点G、H在⊙O的劣弧![]() 上,GH交OC于点E.试求图中阴影部分的面积.(结果保留π)
上,GH交OC于点E.试求图中阴影部分的面积.(结果保留π)
查看答案和解析>>
科目:初中数学 来源: 题型:
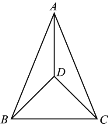
【题目】如图,在△ABC中,AB=AC,D是三角形内一点,连接AD,BD,CD,∠BDC=90°,∠DBC=45°.
(1)求证:∠BAD=∠CAD;
(2)求∠ADB的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
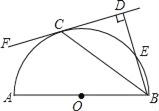
【题目】如图,AB是半圆O的直径,C是半圆O上的一点,CF切半圆O于点C,BD⊥CF于为点D,BD与半圆O交于点E.
(1)求证:BC平分∠ABD.
(2)若DC=8,BE=4,求圆的直径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某数学兴趣小组在本校九年级学生中以“你最喜欢的项体育运动"为主体进行了抽样调查,并将调查结果绘制成下表和下图.
项目 | 篮球 | 乒乓球 | 羽毛球 | 跳绳 | 其他 |
人数 |
| 12 | 10 | 5 | 8 |

请根据图表中的信息完成下列各题:
(1)本次共调查学生______名;
(2)![]() =______;
=______;
(3)在扇形图中,“跳绳”对应的扇形圆是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
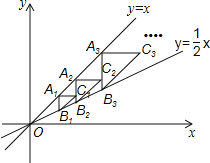
【题目】如图,![]() 点在直线
点在直线![]() 上,过点
上,过点![]() 作
作![]() 轴交直线
轴交直线![]() 于点
于点![]() ,以点
,以点![]() 为直角顶点,
为直角顶点,![]() 为直角边在
为直角边在![]() 的右侧作等腰直角
的右侧作等腰直角![]() ,再过点
,再过点![]() 作
作![]() 轴,分别交直线
轴,分别交直线![]() 和
和![]() 于
于![]() 两点,以点
两点,以点![]() 为直角项点,
为直角项点,![]() 为直角边在
为直角边在![]() 的右侧作等腰直角
的右侧作等腰直角![]() …,按此规律进行下去,则等腰直角
…,按此规律进行下去,则等腰直角![]() 的面积为___. (用含正整数
的面积为___. (用含正整数![]() 的代数式表示)
的代数式表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 网格中,每个小正方形的边长都为
网格中,每个小正方形的边长都为![]() .
.
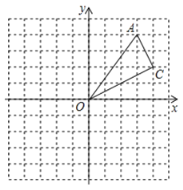
(1)建立如图所示的平面直角坐标系,若点![]() ,则点
,则点![]() 的坐标_______________;
的坐标_______________;
(2)将![]() 向左平移
向左平移![]() 个单位,向上平移
个单位,向上平移![]() 个单位,则点
个单位,则点![]() 的坐标变为_____________;
的坐标变为_____________;
(3)若将![]() 的三个顶点的横纵坐标都乘以
的三个顶点的横纵坐标都乘以![]() ,请画出
,请画出![]() ;
;
(4)图中格点![]() 的面积是_________________;
的面积是_________________;
(5)在![]() 轴上找一点
轴上找一点![]() ,使得
,使得![]() 最小,请画出点
最小,请画出点![]() 的位置,并直接写出
的位置,并直接写出![]() 的最小值是______________.
的最小值是______________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com