Question

如图，在正方形网络中，△ABC的三个顶点都在格点上，点A、B、C的坐标分别为（－2，4）、（－2，0）、（－4，1），结合所给的平面直角坐标系解答下列问题：

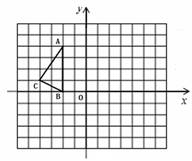
（1）画出△ABC关于原点O对称的△A₁B₁C₁；

（2）平移△ABC，使点A移动到点A₂（0，2），画出平移后的△A₂B₂C₂并写出点B₂、C₂的坐标；

（3）△A₁B₁C₁与△A₂B₂C₂成中心对称，写出其对称中心的坐标．

 

Answer 1

【答案】

(1)详见解析；（2）B₂（0，-2），C₂（-2，-1），作图见解析；（3）H(1,-1).

【解析】

试题分析：（1）画一个三角形关于原点对称的图形，只要画出三个顶点关于原点对称的对称点，然后连接这三个点即可，例如点A（-2,4），连接AO并延长至点A₁，使得AO=A₁O，点A₁就是点A关于原点对称的对称点，点B，点C依次类推，可以得到B₁，点C₁，顺次连接点A₁，点B₁，点C₁，△A₁B₁C₁为所求；（2）将点A移到点A₂（0，2），实际上是先向右移动2个单位长度，在向下移动两个单位长度，将三角形向右移到2个单位长度，在向下移动两个单位长度，可得到△A₂B₂C₂，从而可以得到点B，点C的对应点点B₂（0，-2），点C₂（-2，-1）；（3）两个图形的对称中心是任意两组对应点连线的交点，连接A₁ A₂，C₁C₂交于点H，点H就是△A₁B₁C₁与△A₂B₂C₂的对称中心，H（1，-1）.

试题解析：

（1）如图：

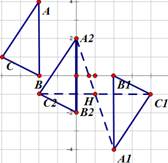
（2）△A₂B₂C₂如图，B₂（0，-2），点C₂（-2，-1）.

（3）连接A₁ A₂，C₁C₂交于点H，点H就是△A₁B₁C₁与△A₂B₂C₂的对称中心，从图中可以观察到点H为格点，H（1，-1）.

考点：1.一个图形关于原点中心对称的作图；2.平移的作图;3.中心对称图形的对称中心的作法.