
【题目】已知:如图,在△ABC中,AB=AC,以AB为直径的⊙O交BC于点D,过点D作DE⊥AC于点E.
(1)求证:DE是⊙O的切线;
(2)若∠CAB=120°,⊙O的半径等于5,求线段BC的长.
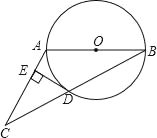
【答案】(1) 见解析;(2)![]()
【解析】试题分析:(1)先连接OD、AD,由于AB是直径以及AB=AC,易证BD=CD,而OA=OB,从而可知OD是△ABC的中位线,那么OD∥AC,再结合DE⊥AC,易证∠ODE=∠CED=90°,即DE是⊙O的切线;
(2)由⊙O半径是5,可知AB=10,而△ABC是等腰三角形,且AD⊥BC,利用等腰三角形三线合一定理可知∠CAD=∠BAD=60°,在Rt△ADB中,易求BD,进而可求BC.
试题解析:如图所示,连接OD、AD.
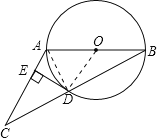
∵AB是直径,
∴∠BDA=∠CDA=90°,
又∵AB=AC,
∴BD=CD,
∵OA=OB,
∴OD是△ABC的中位线,
∴OD∥AC,
∵DE⊥AC,
∴∠ODE=∠CED=90°,
∴DE是⊙O的切线;
(2)∵⊙O半径是5,
∴AB=10,
∵△ABC是等腰三角形,且AD⊥BC,
∴∠CAD=∠BAD=60°,
在Rt△ADB中,BD=sin60°AB=5![]() ,
,
∴BC=10![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
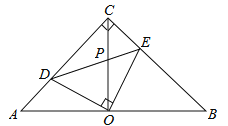
【题目】如图,在等腰直角△ACB中,∠ACB=90°,O是斜边AB的中点,点D、E分别在直角边AC、BC上,且∠DOE=90°,DE交OC于点P.则下列结论:
(1)图形中全等的三角形只有两对;
(2)△ABC的面积等于四边形CDOE的面积的2倍;
(3)CD+CE=![]() OA;
OA;
(4)AD2+BE2=2OPOC.其中正确的结论有( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把下列各数填入相应的横线上:
-2,2π,![]() ,0,-3.7,
,0,-3.7,![]() ,0.35,
,0.35,![]()
整数:______________________; 正有理数:__________________;
无理数:____________________; 负分数:_____________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
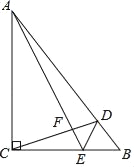
【题目】如图,△ABC,∠ACB=90°,点D,E分别在AB,BC上,AC=AD,∠CDE=45°,CD与AE交于点F,若∠AEC=∠DEB,CE=![]() ,则CF=______.
,则CF=______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】A、B两辆汽车同时从相距330千米的甲、乙两地相向而行,s(千米)表示汽车与甲地的距离,t(分)表示汽车行驶的时间,如图,L1,L2分别表示两辆汽车的s与t的关系.
(1)L1表示哪辆汽车到甲地的距离与行驶时间的关系?
(2)汽车B的速度是多少?
(3)求L1,L2分别表示的两辆汽车的s与t的关系式.
(4)2小时后,两车相距多少千米?
(5)行驶多长时间后,A、B两车相遇?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义一种新运算:观察下列式:
1⊙3=1×4+3=7 3⊙(﹣1)=3×4﹣1=11 5⊙4=5×4+4=24 4⊙(﹣3)=4×4﹣3=13
(1)请你想一想:a⊙b= ;
(2)若a≠b,那么a⊙b b⊙a(填入“=”或“≠” )
(3)若a⊙(﹣2b)=3,请计算 (a﹣b)⊙(2a+b)的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,AB=6,∠DAB=60°,AE分别交BC、BD于点E、F,CE=2,连接CF,以下结论:①△ABF≌△CBF;②点E到AB的距高是![]() ;③AF=CF;④△ABF的面积为
;③AF=CF;④△ABF的面积为![]() 其中一定成立的有( )个.
其中一定成立的有( )个.
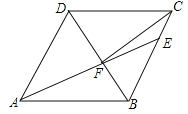
A. 1B. 2C. 3D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某水果商店经销一种苹果,共有20筐,以每筐25千克为标准,超过或不足的千克数分别用正、负数来表示,记录如表:
与标准质量的差值(单位;千克) | -3 | -2 | -1.5 | 0 | 1 | 2.5 |
筐数 | 1 | 4 | 2 | 3 | 2 | 8 |
(1)这20筐苹果中,最重的一筐比最轻的一筐多重多少千克?
(2)与标准重量比较,这20筐苹果总计超过或不足多少千克?
(3)若苹果每千克售价![]() 元,则出售这20筐苹果可卖多少元?
元,则出售这20筐苹果可卖多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com