
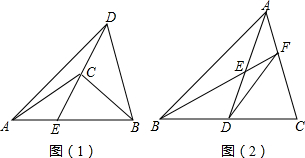
 有下列四个判断:①AD=BF;②AE=BC;③∠EFA=∠CDB;④AE∥BC.请你以其中三个作为题设,余下一个作为结论,写出一个真命题并加以证明.
有下列四个判断:①AD=BF;②AE=BC;③∠EFA=∠CDB;④AE∥BC.请你以其中三个作为题设,余下一个作为结论,写出一个真命题并加以证明.科目:初中数学 来源: 题型:
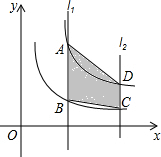 如图,直线AB分别交双曲线y=
如图,直线AB分别交双曲线y=| k |
| x |
| 1 |
| x |
| k |
| x |
| 1 |
| x |
| 9 |
| 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| 1 |
| 4 |
| 1 |
| n |
| 180° |
| n |
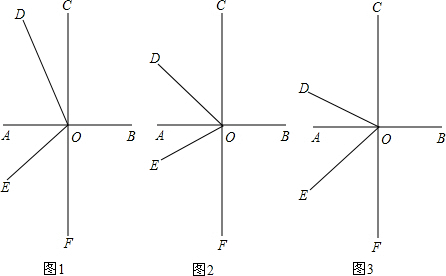
查看答案和解析>>
科目:初中数学 来源: 题型:
A、
| ||||
| B、ax2+bx+c=0 | ||||
| C、x2+2x=x2-1 | ||||
| D、3(x+1)2=2(x+1) |
查看答案和解析>>
科目:初中数学 来源: 题型:
| S△ABC |
| S△ABD |
| CE |
| DE |
| 1 |
| 3 |
| AF |
| CF |
查看答案和解析>>
科目:初中数学 来源: 题型:
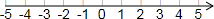 我们知道:|a|的几何意义可以理解为数轴上表示数a的点与原点之间的距离,请大家运用相关知识继续探索数轴上多个点之间的距离问题:
我们知道:|a|的几何意义可以理解为数轴上表示数a的点与原点之间的距离,请大家运用相关知识继续探索数轴上多个点之间的距离问题:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com