Question

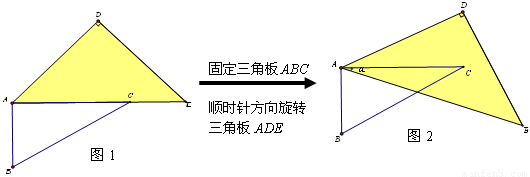
小明是积极思考，喜欢探究问题的同学。一天，如图1，他将直角三角板ABC（∠ACB=30°，∠ABC=60°）和直角三角板ADE（∠DAE=∠DEA=45°）摆放在一起；如图2，固定三角板ABC，将三角板ADE绕点A顺时针方向旋转，记旋转角为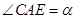  

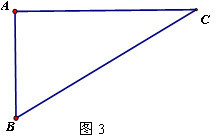
（1）当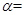_____时，AD∥BC，在图3中画出相应图形；

（2）若当三角板ADE绕点A顺时针方向旋转过程中，两三角板某一边平行（不共线）。例如，如图4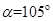，，此时DE∥BC，请你写出除（1）和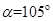情况以外，两三角板某一边平行（不共线）时，的所有可能的度数________________.

 

 

Answer 1

【答案】

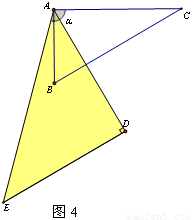
（1）15°，如下图；（2）45°，135°，150°

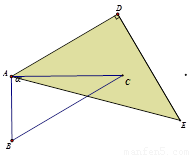
【解析】

试题分析：（1）根据AD∥BC，再根据三角板的度数即可求出α的度数；

（2）要分5种情况进行讨论，分别画出图形，再分别计算出度数即可.

解：（1）∵AD∥BC，

∴∠FGC=∠D=90°，

∵∠C=30°，

∴∠AFD=∠CFG=60°，

∴∠DAF=30°，

∵∠DAE=45°，

∴∠CAE=15°，

∴当α为 15度时，AD∥BC

；

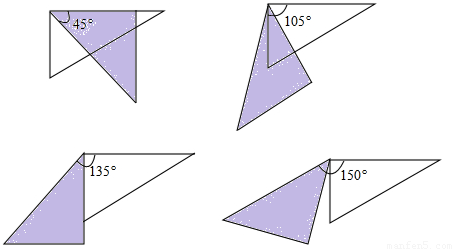
（2）当△ADE的一边与△ABC的某一边平行（不共线）时，旋转角α的所有可能的度数是：15°，45°，105°，135°，150°；

考点：旋转的性质

点评：解题的关键是熟练掌握旋转的性质：旋转变化前后，对应点到旋转中心的距离相等以及每一对对应点与旋转中心连线所构成的旋转角相等．