
 探究:我们把过(1,0)且平行于y轴的直线记为x=1,那么过(0,-1)且平行于x轴的直线则记为x=-1;
探究:我们把过(1,0)且平行于y轴的直线记为x=1,那么过(0,-1)且平行于x轴的直线则记为x=-1;分析 探究:利用x=1以及y=2,x=-3的意义分别分析得出答案;
(1)利用坐标系结合对称性分别得出符合题意的答案;
(2)利用坐标系结合对称性分别得出符合题意的答案.
解答  解:探究:我们把过(1,0)且平行于y轴的直线记为:x=1,
解:探究:我们把过(1,0)且平行于y轴的直线记为:x=1,
那么过(0,-1)且平行于x轴的直线则记为:x=-1;
直线y=2在平面直角坐标系中的位置为:过(0,2)平行于x轴的直线;
则直线x=-3在平面直角坐标系中的位置为:过(-3,0)平行于y轴的直线.
故答案为:x=1,x=-1,过(0,2)平行于x轴的直线;过(-3,0)平行于y轴的直线;
(1)M(2,3)关于直线x=1的对称点的坐标为:(0,3);
关于直线y=-2的对称点的坐标为:(2,-7);
点N(-2,3)关于直线x=-1的对称点的坐标为:(0,3);
关于直线y=2的对称点的坐标为:(-2,1).
故答案为:(0,3),(2,-7),(0,3),(-2,1);
(2)点M(-2,-3)与N(-2,-5)关于直线y=-4对称,
点M(-3,-2)与N(-5,-2)关于直线x=-4对称.
故答案为:y=-4,x=-4.
点评 此题主要考查了坐标与图形的性质以及点的对称性,结合坐标系得出对称点是解题关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
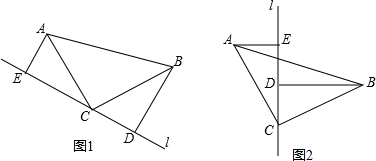
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,若$\frac{AD}{BD}$=$\frac{AE}{EC}$,则$\frac{AD}{AB}$=$\frac{AE}{AC}$.说明理由.
如图,若$\frac{AD}{BD}$=$\frac{AE}{EC}$,则$\frac{AD}{AB}$=$\frac{AE}{AC}$.说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图是一张矩形纸片ABCD,E,F分别是BC,AD上的点,(但不与顶点重合),如果直线EF将矩形分成面积相等的两部分;
如图是一张矩形纸片ABCD,E,F分别是BC,AD上的点,(但不与顶点重合),如果直线EF将矩形分成面积相等的两部分; 查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com