
【题目】如图,一次函数y=kx+b与反比例函数y= ![]() 的图象交于A(1,4),B(4,n)两点.
的图象交于A(1,4),B(4,n)两点. 
(1)求反比例函数的解析式;
(2)求一次函数的解析式;
(3)点P是x轴上的一动点,当PA+PB最小时,求点P的坐标.
【答案】
(1)解:把A(1,4)代入y= ![]() ,得:m=4,
,得:m=4,
∴反比例函数的解析式为y= ![]()
(2)解:把B(4,n)代入y= ![]() ,得:n=1,
,得:n=1,
∴B(4,1),
把A(1,4)、(4,1)代入y=kx+b,得: ![]() ,
,
解得: ![]() ,
,
∴一次函数的解析式为y=﹣x+5
(3)解:作B的对称点B′,连接AB′,交x轴于P,此时PA+PB=AB′最小,
∵B(4,1),
∴B′(4,﹣1),
设直线AB′的解析式为y=mx+n,
∴ ![]() ,解得
,解得 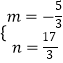 ,
,
∴直线AB′的解析式为y=﹣ ![]() x+
x+ ![]() ,
,
令y=0,得﹣ ![]() x+
x+ ![]() =0,
=0,
解得x= ![]() ,
,
∴点P的坐标为( ![]() ,0).
,0).
【解析】(1)将点A(1,4)代入反比例函数解析式可得其解析式;(2)先根据反比例函数解析式求得点B坐标,再由A、B坐标可得直线解析式;(3)作B的对称点B′,连接AB′,交x轴于P,此时PA+PB=AB′最小,根据B的坐标求得B′的坐标,然后根据待定系数法求得直线AB′的解析式,进而求得与x轴的交点即可.
【考点精析】解答此题的关键在于理解轴对称-最短路线问题的相关知识,掌握已知起点结点,求最短路径;与确定起点相反,已知终点结点,求最短路径;已知起点和终点,求两结点之间的最短路径;求图中所有最短路径.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,O为直线AB上一点,∠AOC=50°,OD平分∠AOC,∠DOE=90°.
(1)请你数一数,图中有多少个小于平角的角;
(2)求出∠BOD的度数;
(3)请通过计算说明OE是否平分∠BOC.

查看答案和解析>>
科目:初中数学 来源: 题型:
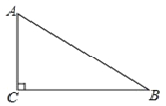
【题目】如图,在 ABC ,C 90,AC<BC,D 为 BC 上一点,且到 A、B 两点的距离相等.
(1)用直尺和圆规,作出点 D 的位置(不写作法,保留作图痕迹);
(2)连结 AD,若 B 36 ,求∠CAD 的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,AB=6,AD=9,∠BAD的平分线交BC于点E,交DC的延长线于点F,BG⊥AE,垂足为G.若BG=4![]() ,则△CEF的面积是( )
,则△CEF的面积是( )

A. ![]() B. 2
B. 2![]() C. 3
C. 3![]() D. 4
D. 4![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一楼房AB后有一假山,其坡度为i=1: ![]() ,山坡坡面上E点处有一休息亭,测得假山坡脚C与楼房水平距离BC=25米,与亭子距离CE=20米,小丽从楼房顶测得E点的俯角为45°,求楼房AB的高.(注:坡度i是指坡面的铅直高度与水平宽度的比)
,山坡坡面上E点处有一休息亭,测得假山坡脚C与楼房水平距离BC=25米,与亭子距离CE=20米,小丽从楼房顶测得E点的俯角为45°,求楼房AB的高.(注:坡度i是指坡面的铅直高度与水平宽度的比) 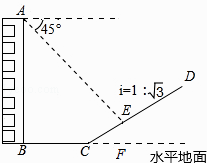
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于x的一元二次方程x2+(2k+1)x+k2+1=0有两个不等实根x1、x2.
(1)求实数k的取值范围.
(2)若方程两实根x1、x2满足x1+x2=﹣x1x2,求k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
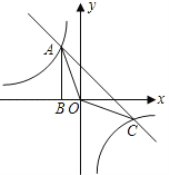
【题目】如图,Rt△ABO的顶点A是双曲线y1=![]() 与直线y2=-x-(k+1)在第二象限的交点.AB⊥x轴于B,且S△ABO=
与直线y2=-x-(k+1)在第二象限的交点.AB⊥x轴于B,且S△ABO=![]() .
.
(1)求这两个函数的解析式;
(2)求△AOC的面积.
(3)直接写出使y1>y2成立的x的取值范围
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们把对角线互相垂直的四边形叫做垂美四边形.
(1)(概念理解)在平行四边形、矩形、菱形、正方形中,一定是垂美四边形的是___________.
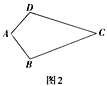
(2)(性质探究)如图2,试探索垂美四边形ABCD的两组对边AB,CD与BC ,AD之间的数量关系,写出证明过程。
(3)(问题解决)如图3,分别以Rt△ACB的直角边AC和斜边AB为边向外做正方形ACFG和正方形ABDE,连接CE,BG,GE, 已知AC=![]() ,BC=1 求GE的长.
,BC=1 求GE的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com