
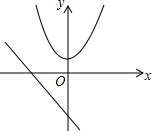
 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,给出以下四个结论:①a-c<0;②c-ab<0;③a-b+c>0;④a+b+c>0,其中所有正确结论的序号是( )
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,给出以下四个结论:①a-c<0;②c-ab<0;③a-b+c>0;④a+b+c>0,其中所有正确结论的序号是( )| A、②④ | B、②③④ |
| C、①②④ | D、①④ |


 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案科目:初中数学 来源: 题型:
| A、2.5×106 |
| B、2.5×107 |
| C、0.25×107 |
| D、25×105 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,在等腰直角△ABC中,∠C=90°,O是斜边AB的中点,将直角三角板的直角顶点与点O重合,两直角边分别与边AC、BC交于点E、F,试判断AE与CF的数量关系,并进行证明.
如图,在等腰直角△ABC中,∠C=90°,O是斜边AB的中点,将直角三角板的直角顶点与点O重合,两直角边分别与边AC、BC交于点E、F,试判断AE与CF的数量关系,并进行证明.查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,坐标系中有抛物线c:y=x2+m和直线l:y=-2x-2.
如图,坐标系中有抛物线c:y=x2+m和直线l:y=-2x-2.查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
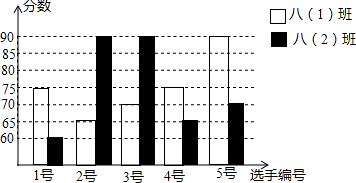
| 平均数(分) | 中位数(分) | 极差(分) | 方差 | |
| 八(1)班 | 75 | 25 | ||
| 八(2)班 | 75 | 70 | 160 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com