练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    已知AB＝CD，DE＝BF，AE＝CF，求证：DE∥BF

    答案：
    解析：

    因为AE＝CF，所以AE＋EF＝CF＋FE，即AF＝CE，又因为AB＝CD，DE＝BF，所以△CDE≌△ABF，所以∠DEC＝∠BFA，所以DE∥BF


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：1+1轻巧夺冠·优化训练(冀教版)七年级数学(下) 冀教版银版 题型：047

    如图所示，已知AB＝CD，DE⊥AC，BF⊥AC，垂足分别是E、F，∠B＝∠D．

    求证：AF＝CE．

    查看答案和解析>>

    科目：初中数学 来源：学习周报　数学　沪科八年级版　2009－2010学年　第17期　总173期 沪科版 题型：047

    如图，已知BD＝CD，DE⊥AB，DF⊥AC，垂足分别为E、F，∠EDB＝∠FDC．

    求证：点D在∠BAC的平分线上．

    查看答案和解析>>

    科目：初中数学 来源：同步练习数学　　九年级上册 题型：022

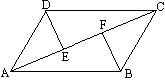
    如图所示，AB∥CD，AB＝CD，DE⊥AC，BF⊥AC，垂足分别是E、F，要证明△ADC≌△CBA，已知AB＝CD，CA＝AC，又可由AB∥CD，得∠________＝∠________，根据________即可证得．

    查看答案和解析>>

    科目：初中数学 来源： 题型：044

    如图，△DEC和△BFA都是直角三角形，∠DEC＝∠BFA＝90°.

    (1)已知AB＝CD，DE＝BF，求证：AE＝CF，AB∥CD；

    (2)如果AE＝CF，AB∥CD，那么AB＝CD，DE＝BF吗？

    查看答案和解析>>

    同步练习册答案