
【题目】计算:2sin45°﹣( ![]() )0
)0 ![]() .
.
【答案】解:原式=2× ![]() ﹣1+2+
﹣1+2+ ![]() ﹣1=2
﹣1=2 ![]()
【解析】原式第一项利用特殊角的三角函数值计算,第二项利用零指数幂法则计算,第三项利用负整数指数幂法则计算,最后一项利用绝对值的代数意义化简,计算即可得到结果.
【考点精析】本题主要考查了零指数幂法则和整数指数幂的运算性质的相关知识点,需要掌握零次幂和负整数指数幂的意义: a0=1(a≠0);a-p=1/ap(a≠0,p为正整数);aman=am+n(m、n是正整数);(am)n=amn(m、n是正整数);(ab)n=anbn(n是正整数);am/an=am-n(a不等于0,m、n为正整数);(a/b)n=an/bn(n为正整数)才能正确解答此题.


科目:初中数学 来源: 题型:
【题目】甲、乙两地相距720km,一列快车和一列慢车都从甲地驶往乙地,慢车先行驶1小时后,快车才开始行驶.已知快车的速度是120km/h,慢车的速度是80km/h,快车到达乙地后,停留了20min,由于有新的任务,于是立即按原速返回甲地.在快车从甲地出发到回到甲地的整个程中,与慢车相遇了两次,这两次相遇时间间隔是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,以点A(1,0)为圆心,以2为半径的圆与x轴交于B,C两点,与y轴交于D,E两点.
(1)直接写出B,C,D点的坐标;
(2)若B、C、D三点在抛物线y=ax2+bx+c上,求出这个抛物线的解析式及它的顶点坐标.
(3)若圆A的切线交x轴正半轴于点M,交y轴负半轴于点N,切点为P,∠OMN=30°,试判断直线MN是否经过B、C、D三点所在抛物线的顶点?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,OE平分∠AOC,OF平分∠BOC,且∠BOC=60°,若∠AOC+∠EOF=156°,则∠EOF的度数是( )

A. 88° B. 30° C. 32° D. 48°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,关于x的二次函数y=x2﹣x+m的图象交x轴的正半轴于A,B两点,交y轴的正半轴于C点,如果x=a时,y<0,那么关于x的一次函数y=(a﹣1)x+m的图象可能是( ) 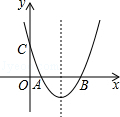
A.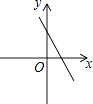
B.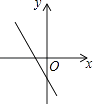
C.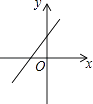
D.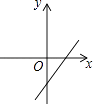
查看答案和解析>>
科目:初中数学 来源: 题型:
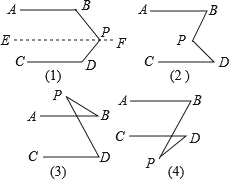
【题目】如图(1),AB∥CD,试求∠BPD与∠B、∠D的数量关系,说明理由.
(1)填空:
解:过点P作EF∥AB,
∴∠B+∠BPE=180°
∵AB∥CD,EF∥AB
∴ (如果两条直线都和第三条直线平行,那么这两条直线也互相平行)
∠EPD+ =180°
∴∠B+∠BPE+∠EPD+∠D=360°
∴∠B+∠BPD+∠D=360°
(2)依照上面的解题方法,观察图(2),已知AB∥CD,猜想图中的∠BPD与∠B、∠D的数量关系,并说明理由.
(3)观察图(3)和(4),已知AB∥CD,直接写出图中的∠BPD与∠B、∠D的数量关系,不用说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】校车安全是近几年社会关注的重大问题,安全隐患主要是超速和超载.某中学数学活动小组设计了如下检测公路上行驶的汽车速度的实验:先在公路旁边选取一点C,再在笔直的车道L上确定点D,使CD与L垂直,测得CD的长等于24米,在L上点D的同侧取点A、B,使∠CAD=30°,∠CBD=60°. 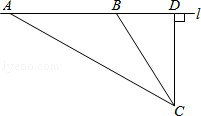
(1)求AB的长(结果保留根号);
(2)已知本路段对校车限速为45千米/小时,若测得某辆校车从A到B用时2秒,这辆校车是否超速?说明理由.(参考数据: ![]() ≈1.73,
≈1.73, ![]() ≈1.41)
≈1.41)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,将边长为1的正方形ABCD压扁为边长为1的菱形ABCD.在菱形ABCD中,∠A的大小为α,面积记为S.

(1)请补全下表:
30° | 45° | 60° | 90° | 120° | 135° | 150° | |
S |
| 1 |
|
(2)填空:
由(1)可以发现正方形在压扁的过程中,菱形的面积随着∠A大小的变化而变化,不妨把菱形的面积S记为S(α).例如:当α=30°时,![]() ;当α=135°时,
;当α=135°时,![]() .由上表可以得到
.由上表可以得到![]() ( ______°);
( ______°);![]() ( ______°),…,由此可以归纳出
( ______°),…,由此可以归纳出![]() .
.
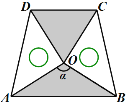
(3) 两块相同的等腰直角三角板按如图的方式放置,AD=![]() ,∠AOB=α,试探究图中两个带阴影的三角形面积是否相等,并说明理由(注:可以利用(2)中的结论).
,∠AOB=α,试探究图中两个带阴影的三角形面积是否相等,并说明理由(注:可以利用(2)中的结论).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB⊥AC,AD⊥BC,点D是BC的中点,DE⊥AB,DF⊥AC,连接EF,则图中等腰直角三角形的个数是( )
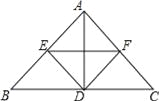
A. 8个 B. 10个 C. 12个 D. 13个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com