
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 13 | B. | -1 | C. | -$\frac{7}{3}$ | D. | 1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
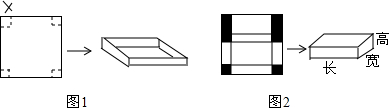
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,∠MON=30°,点A1、A2、A3…在射线ON上,点B1、B2、B3…在射线OM上,△A1B1A2、△A2B2A3、△A3B3A4…均为等边三角形,从左起第1个等边三角形的边长记a1,第2个等边三角形的长记为a2,以此类推,若OA1=3,则a2=6,a2015=3×22014.
如图,∠MON=30°,点A1、A2、A3…在射线ON上,点B1、B2、B3…在射线OM上,△A1B1A2、△A2B2A3、△A3B3A4…均为等边三角形,从左起第1个等边三角形的边长记a1,第2个等边三角形的长记为a2,以此类推,若OA1=3,则a2=6,a2015=3×22014.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 球队数(n) | 2 | 3 | 4 | 5 | 6 |
| 比赛场数 | 1 | 3 | 6 | 10 | 15 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
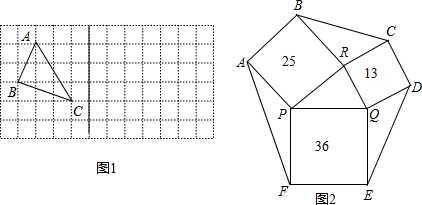
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com