(2002•大连)阅读材料,解答问题.
当抛物线的表达式中含有字母系数时,随着系数中的字母取值的不同,抛物线的顶点坐标出将发生变化.
例如:由抛物线y=x2-2mx+m2+2m-1,…①
有y=(x-m)2+2m-1,…②
∴抛物线的顶点坐标为(m,2m-1)
即x=m …③
y=2m-1 …④
当m的值变化时,x、y的值也随之变化,因而y值也随x值的变化而变化
将③代入④,得y=2x-1…⑤
可见,不论m取任何实数,抛物线顶点的纵坐标y和横坐标x都满足关系式y=2x-1.
解答问题:
(1)在上述过程中,由①到②所用的数学方法是______,由③、④到⑤所用到的数学方法是______.
(2)根据阅读材料提供的方法,确定抛物线y=x2-2mx+2m2-3m+1顶点的纵坐标y与横坐标x之间的表达式.
【答案】
分析:(1)配方法是指把含自变量的项配成完全平方式,代入消元法用含一个字母的式子代替另外一个字母;
(2)用配方法把抛物线的一般式写成顶点式,从而得出顶点坐标,用x代替m,可得顶点的纵坐标y与横坐标x之间的表达式.
解答:解:(1)配方法,代入消元法.
(2)变形配方得y=x
2-2mx+m
2+m
2-3m+1=(x-m)
2+m
2-3m+1,
∴抛物线的顶点坐标为(m,m
2-3m+1),
即
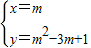
,
代入消元得y=x
2-3x+1.
点评:本题考查了抛物线解析式变形的重要方法:配方法,再考虑用消元法得出顶点的纵坐标y与横坐标x之间的表达式.

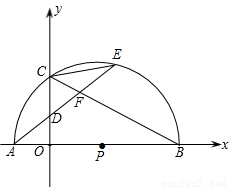
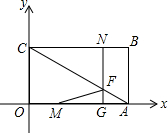 在平面直角坐标系中,已知两点坐标P1(x1,y1)P2(x2,y2)我们就可以使用两点间距离公式P1P2=
在平面直角坐标系中,已知两点坐标P1(x1,y1)P2(x2,y2)我们就可以使用两点间距离公式P1P2=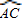 =
=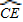 ,
, ,tan∠ECB=
,tan∠ECB= ,求经过A、B、C三点的抛物线的解析式;
,求经过A、B、C三点的抛物线的解析式; AE,是否存在过点M的直线,使该直线与(2)中所得的抛物线的两个交点到y轴距离相等?若存在,求出这条直线的解析式;若不存在,请说明理由.
AE,是否存在过点M的直线,使该直线与(2)中所得的抛物线的两个交点到y轴距离相等?若存在,求出这条直线的解析式;若不存在,请说明理由.