
【题目】如图,四边形ABCD内接于⊙O,点E在CB的延长线上,连接AC,AE,∠ACB=∠BAE=45°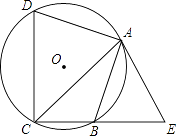
(1)求证:AE是⊙O的切线;
(2)若 AB=AD,AC=2 ![]() ,tan∠ADC=3,求CD的长.
,tan∠ADC=3,求CD的长.
【答案】
(1)
证明:
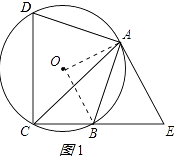
连接OA、OB,如图1所示:
∵∠ACB=45°,
∴∠AOB=2∠ACB=90°,
∵OA=OB,
∴∠OAB=∠OBA=45°,
∵∠BAE=45°,
∴∠OAE=∠OAB+∠BAE=90°,
∴AE⊥OA,
∴AE是⊙O的切线
(2)
解:
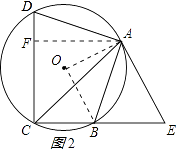
作AF⊥CD于F,如图2所示:
∵AB=AD,
∴ ![]() ,
,
∴∠ACB=∠ACD=45°,
∵AF⊥CD,
∴∠AFC=∠AFD=90°,
∵AC=2 ![]() ,
,
∴在Rt△AFC中,AF=CF=ACsin∠ACF=2 ![]() ×
× ![]() =2,
=2,
∵在Rt△AFD中,tan∠ADC= ![]() =3,
=3,
∴DF= ![]() ,
,
∴CD=CF+DF=2+ ![]() =
= ![]() .
.
【解析】(1)连接OA、OB,由圆周角定理得出∠AOB=2∠ACB=90°,由等腰直角三角形的性质得出∠OAB=∠OBA=45°,求出∠OAE=∠OAB+∠BAE=90°,即可得出结论;(2)作AF⊥CD于F,证出 ![]() ,由圆周角定理得出∠ACB=∠ACD=45°,由三角函数求出AF=CF=ACsin∠ACF=2,DF=
,由圆周角定理得出∠ACB=∠ACD=45°,由三角函数求出AF=CF=ACsin∠ACF=2,DF= ![]() ,即可得出CD的长.
,即可得出CD的长.
【考点精析】认真审题,首先需要了解切线的判定定理(切线的判定方法:经过半径外端并且垂直于这条半径的直线是圆的切线).


科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,点D , E分别在AB , AC上,DE∥BC , AD=CE . 若AB:AC=3:2,BC=10,则DE的长为( ) 
A.3
B.4
C.5
D.6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一元二次方程x2-x-3=0的较小根为x1 , 则下面对x1的估计正确的是( )
A.-2< x1<-1
B.-3< x1<-2
C.2< x1<3
D.-1< x1<0
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列方程或方程组解应用题:
为祝贺北京成功获得2022年冬奥会主办权,某工艺品厂准备生产纪念北京申办冬奥会成功的“纪念章”和“冬奥印”.生产一枚“纪念章”需要用甲种原料4盒,乙种原料3盒;生产一枚“冬奥印”需要用甲种原料5 盒,乙种原料10 盒.该厂购进甲、乙两种原料分别为20000盒和30000盒,如果将所购进原料正好全部都用完,那么能生产“纪念章”和“冬奥印”各多少枚?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,点A的坐标为(1,0),P是第一象限内任意一点,连接PO,PA,若∠POA=m°,∠PAO=n°,则我们把(m°,n°)叫做点P 的“双角坐标”.例如,点(1,1)的“双角坐标”为(45°,90°).
(1)点( ![]() ,
, ![]() )的“双角坐标”为;
)的“双角坐标”为;
(2)若点P到x轴的距离为 ![]() ,则m+n的最小值为 .
,则m+n的最小值为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系 xOy中,对于点P(x,y),以及两个无公共点的图形W1和W2 , 若在图形W1和W2上分别存在点M (x1 , y1 )和N (x2 , y2 ),使得P是线段MN的中点,则称点M 和N被点P“关联”,并称点P为图形W1和W2的一个“中位点”,此时P,M,N三个点的坐标满足x= ![]() ,y=
,y= ![]()
(1)已知点A(0,1),B(4,1),C(3,﹣1),D(3,﹣2),连接AB,CD.
①对于线段AB和线段CD,若点A和C被点P“关联”,则点P的坐标为;
②线段AB和线段CD的一“中位点”是Q (2,﹣ ![]() ),求这两条线段上被点Q“关联”的两个点的坐标;
),求这两条线段上被点Q“关联”的两个点的坐标;
(2)如图1,已知点R(﹣2,0)和抛物线W1:y=x2﹣2x,对于抛物线W1上的每一个点M,在抛物线W2上都存在点N,使得点N和M 被点R“关联”,请在图1 中画出符合条件的抛物线W2;
(3)正方形EFGH的顶点分别是E(﹣4,1),F(﹣4,﹣1),G(﹣2,﹣1),H(﹣2,1),⊙T的圆心为T(3,0),半径为1.请在图2中画出由正方形EFGH和⊙T的所有“中位点”组成的图形(若涉及平面中某个区域时可以用阴影表示),并直接写出该图形的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】研究几何图形,我们往往先给出这类图形的定义,再研究它的性质和判定方法.我们给出如下定义:如图,四边形ABCD中,AB=AD,CB=CD像这样两组邻边分别相等的四边形叫做“筝形”;
(1)小文认为菱形是特殊的“筝形”,你认为他的判断正确吗?
(2)小文根据学习几何图形的经验,通过观察、实验、归纳、类比、猜想、证明等方法,对AB≠BC的“筝形”的性质和判定方法进行了探究.下面是小文探究的过程,请补充完成:
①他首先发现了这类“筝形”有一组对角相等,并进行了证明,请你完成小文的证明过程.
已知:如图,在”筝形”ABCD中,AB=AD,CB=CD.
求证:∠ABC=∠ADC.
证明:②小文由①得到了这类“筝形”角的性质,他进一步探究发现这类“筝形”还具有其它性质,请再写出这类“筝形”的一条性质(除“筝形”的定义外);
③继性质探究后,小文探究了这类“筝形”的判定方法,写出这类“筝形”的一条判定方法(除“筝形”的定义外):
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下表给出了代数式x2+bx+c与x的一些对应值:
x | … | 0 | 1 | 2 | 3 | 4 | … |
x2+bx+c | … | 3 | ﹣1 | 3 | … |
(1)请在表内的空格中填入适当的数;
(2)设y=x2+bx+c,则当x取何值时,y>0;
(3)请说明经过怎样平移函数y=x2+bx+c的图象得到函数y=x2的图象?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com