
【题目】如图,在矩形![]() 中,
中,![]() ,点
,点![]() 从点
从点![]() 出发,沿
出发,沿![]() 向点
向点![]() 匀速运动,速度为每秒1个单位,过点
匀速运动,速度为每秒1个单位,过点![]() 作
作![]() ,交对角线
,交对角线![]() 于点
于点![]() .点
.点![]() 从点
从点![]() 出发,沿对角线
出发,沿对角线![]() 向点
向点![]() 匀速运动,速度为每秒1个单位.
匀速运动,速度为每秒1个单位. ![]() 、
、![]() 两点同时出发,设它们的运动时间为
两点同时出发,设它们的运动时间为![]() 秒(
秒(![]() ).
).
(1)当![]() 时,求出
时,求出![]() 的值;
的值;
(2)连接![]() ,当
,当![]() 时,求出
时,求出![]() 的值;
的值;
(3)试探究:当![]() 为何值时,
为何值时,![]() 是等腰三角形?
是等腰三角形?


【答案】(1)t=![]() ;(2)t=
;(2)t=![]() ;(3)满足条件的时间t为
;(3)满足条件的时间t为![]() 或
或![]() 或
或![]() 或
或![]() .
.
【解析】(1)判断出△PBQ∽△DBC得出比例式建立方程即可得出结论;
(2)先判断出△BPM∽△BCD得出比例式求出PM=6-![]() t,BM=10-
t,BM=10-![]() t,再判断出△ADM∽△PBQ,得出比例式建立方程即可得出结论;
t,再判断出△ADM∽△PBQ,得出比例式建立方程即可得出结论;
(3)分两种情况利用等腰三角形的性质即可得出结论.
(1)在矩形ABCD中,AB=CD=6,BC=8,∴∠C=90°,BD=10,
根据题意得,CP=BQ=t,BP=8﹣t,∵PQ⊥BD,∴∠BQP=90°,∴∠BQP=∠C,
∵∠PBQ=∠DBC=45°,∴△PBQ∽△DBC,∴![]() ,∴
,∴![]() ,∴t=
,∴t=![]() ;
;
(2)∵PM⊥BC,∠C=90°,∴PM∥CD,∴△BPM∽△BCD,∴![]() ,
,
∴![]() ,∴PM=6﹣
,∴PM=6﹣![]() t,BM=10﹣
t,BM=10﹣![]() t,∴DM=
t,∴DM=![]() t,
t,
∵PQ∥AM,∴∠AMQ=∠MQP,∴∠AMD=∠PQB,
∵四边形ABCD是矩形,∴AD∥BC,∴∠ADM=∠PBQ,∴△ADM∽△PBQ,
∴![]() ,∴
,∴ ,∴t=
,∴t=![]() ;
;
(3)

①当点Q在线段BM上时,
Ⅰ、若PM=MQ,∴6﹣![]() t=10﹣
t=10﹣![]() t,∴t=
t,∴t=![]() ,
,
Ⅱ、若PM=PQ时,如图1,作PN⊥MQ于N,
∴∠PNM=90°,MN=![]() MQ=
MQ=![]() (10﹣
(10﹣![]() t)=5﹣
t)=5﹣![]() t,∴∠PNM=∠C,
t,∴∠PNM=∠C,
∵PM∥CD,∴∠PMQ=∠BDC,∴△PMN∽△BDC,
∴![]() ,∴
,∴ ,∴t=
,∴t=![]() ,
,
Ⅲ、若MQ=PQ时,如备用图1,作QE⊥PM于E,∴QE∥BP,ME=![]() PM,
PM,
∴△QEM∽△BPM,∴![]() ,∴MQ=BQ,∴10﹣
,∴MQ=BQ,∴10﹣![]() t=t,∴t=
t=t,∴t=![]() ,
,
②当点M在线段BQ上时,如备用图2,∠PMQ是钝角,∴只可能PM=QM,
∴6﹣![]() t=t﹣(10﹣
t=t﹣(10﹣![]() t),∴t=
t),∴t=![]() ,即:满足条件的时间t为
,即:满足条件的时间t为![]() 或
或![]() 或
或![]() 或
或![]() .
.


 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AC=6,BC=8,∠BCA的平分线与AB边的垂直平分线相交于点D,DE⊥AC,DF⊥BC,垂足分别是E、F.
(1)求证:AE=BF;
(2)求AE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】暑期临近,重庆市某中学校为了丰富学生的暑期文化生活,同时帮助孩子融洽亲子关系,增进亲子间的情感交流,计划组织学生去某景区参加为期一周的“亲子一家游”活动. 若报名参加此次活动的学生人数共有56人,其中要求参加的每名学生都至少需要一名家长陪同参加.
(1)假设参加此次活动的家长人数是参加学生人数的2倍少2人,为了此次活动学校专门为每名学生和家长购买一件T恤衫, 家长的T恤衫每购买8件赠送1件学生T恤衫(不足8件不赠送),学生T恤衫每件15元,学校购买服装的费用不超过3401元,请问每件家长T恤衫的价格最高是多少元?
(2)已知该景区的成人票价每张100元,学生票价每张50元,为了支持此次活动,该景区特地推出如下优惠活动:每张成人票价格下调a%,学生票价格下调.![]() a% 另外,经统计此次参加活动的家长人数比学生人数多a%, 参加此次活动的购买票价总费用比未优惠前减少了
a% 另外,经统计此次参加活动的家长人数比学生人数多a%, 参加此次活动的购买票价总费用比未优惠前减少了![]() a%,求a的值.
a%,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
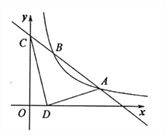
【题目】如图,已知一次函数![]() 的图像与反比例函数
的图像与反比例函数![]() 的图像交于点
的图像交于点![]() 和点
和点![]() ,与
,与![]() 轴交于点
轴交于点![]() .
.
(1)求反比例函数和一次函数的表达式.
(2)若在![]() 轴上有一点
轴上有一点![]() ,其横坐标是1,连接
,其横坐标是1,连接![]() 、
、![]() ,求
,求![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
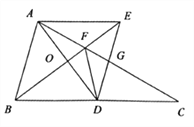
【题目】如图,在![]() 中,
中,![]() 是
是![]() 边上的中线,
边上的中线,![]() 是
是![]() 中点,过点
中点,过点![]() 作
作![]() ,交
,交![]() 的延长线于点
的延长线于点![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() .
.
(1)判断四边形![]() 的形状,并说明理由;
的形状,并说明理由;
(2)若![]() ,且
,且![]() ,求四边形
,求四边形![]() 的面积.
的面积.
(3)连接![]() ,求证:
,求证:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1)所示,∠AOB、∠COD都是直角.
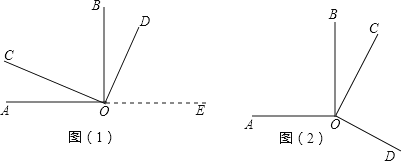
(1)试猜想∠AOD与∠COB在数量上是相等,互余,还是互补的关系.请你用推理的方法说明你的猜想是合理的.
(2)当∠COD绕着点O旋转到图(2)所示位置时,你在(1)中的猜想还成立吗?请你证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知抛物线y=ax2+bx﹣2(a≠0)与x轴交于A(1,0)、B(3,0)两点,与y轴交于点C,其顶点为D. 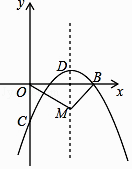
(1)求抛物线的解析式;
(2)一动点M从点D出发,以每秒1个单位的速度沿抛物线的对称轴向下运动,连OM,BM,设运动时间为t秒(t=0),在点M的运动过程中,当∠OMB=90°时,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等边△ABC中,BF是AC边上中线,点D在BF上,连接AD,在AD的右侧作等边△ADE,连接EF,当△AEF周长最小时,∠CFE的大小是( )

A. 30° B. 45° C. 60° D. 90°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com