
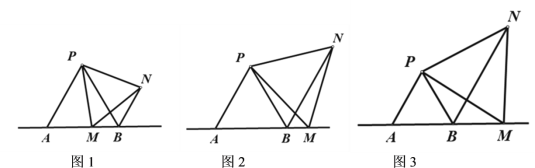
【题目】如图1,点M为直线AB上一动点,△PAB,△PMN都是等边三角形,连接BN,
(1)M点如图1的位置时,如果AM=5,求BN的长;
(2)M点在如图2位置时,线段AB、BM、BN三者之间的数量关系__________________;
(3)M点在如图3位置时,当BM=AB时,证明:MN⊥AB.
【答案】(1)5;(2)AB+BM=BN;(3)详见解析
【解析】
(1)根据等边三角形的性质可得:∠APB=∠MPN,PA=PB,PM=PN,然后即可利用SAS证明△PAM≌△PBN,再利用全等三角形的性质即得结论;
(2)仿(1)的方法利用SAS证明△PAM≌△PBN,可得AM=BN,进一步即得结论;
(3)根据等边三角形的性质、等腰三角形的性质和三角形的外角性质可得∠BPM=∠PMB =30°,易知∠PMN=60°,问题即得解决.
解:(1)如图1,∵△PAB,△PMN都是等边三角形,
∴∠APB=∠MPN=60°,PA=PB,PM=PN,
∴∠APM=∠BPN,
∴△PAM≌△PBN(SAS) ,
∴AM=BN=5,∴BN的长为5;
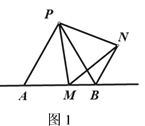
(2) AB+BM=BN;
理由:如图2,∵△PAB,△PMN都是等边三角形,
∴∠APB=∠MPN=60°,PA=PB,PM=PN,
∴∠APM=∠BPN,
∴△PAM≌△PBN(SAS) ,
∴AM=BN,即AB+BM=BN;
故答案为:AB+BM=BN;
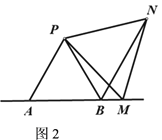
(3)证明:如图3,∵△PAB是等边三角形,∴AB=PB,∠ABP=60°,
∵BM=AB,∴PB=BM,∴∠BPM=∠PMB,
∵∠ABP=60°,∴∠BPM=∠PMB =30°,
∵△PMN是等边三角形,∴∠PMN=60°,
∴∠AMN=90°,即MN⊥AB.


 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案科目:初中数学 来源: 题型:
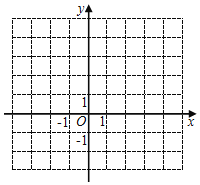
【题目】已知:A(1,0),B(0,4),C(4,2).
(1)在坐标系中描出各点(小正方形网格的长度为单位1),画出△ABC;(三点及连线请加黑描重)
(2)若△A1B1C1与△ABC关于y轴对称,请在图中画出△A1B1C1;
(3)点Q是x轴上的一动点,则使QB+QC最小的点Q坐标为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AE⊥AB且AE=AB,BC⊥CD且BC=CD,请按图中所标注的数据,计算图中实线所围成的面积S是( )

A.50B.62C.65D.68
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,王老师将某班近三个月跳跃类项目的训练情况做了统计,并绘制了折线统计图,则根据图中信息以下判断错误的是( )
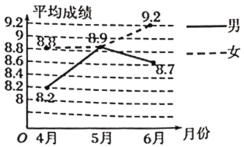
A.男女生5月份的平均成绩一样
B.4月到6月,女生平均成绩一直在进步
C.4月到5月,女生平均成绩的增长率约为![]()
D.5月到6月女生平均成绩比4月到5月的平均成绩增长快
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点B、F、C、E在一条直线上,FB=CE,AB∥ED,AC∥FD;
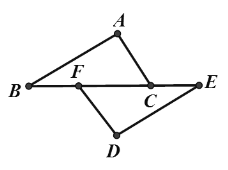
(1)已知∠A=85°,∠ACE=115°,求∠B度数;
(2)求证:AB=DE.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题情境:课堂上,同学们研究几何变量之间的函数关系问题:如图,菱形ABCD的对角线AC,BD相交于点O,AC=4,BD=2.点P是AC上的一个动点,过点P作MN⊥AC,垂足为点P(点M在边AD、DC上,点N在边AB、BC上).设AP的长为x(0≤x≤4),△AMN的面积为y.
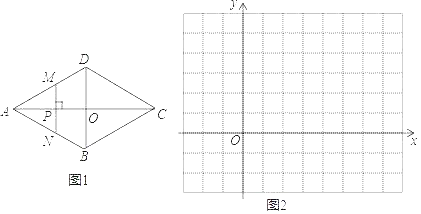
建立模型:(1)y与x的函数关系式为:![]() ,
,
解决问题:(2)为进一步研究y随x变化的规律,小明想画出此函数的图象.请你补充列表,并在如图的坐标系中画出此函数的图象:
x | 0 |
| 1 |
| 2 |
| 3 |
| 4 |
y | 0 |
|
|
|
|
|
|
| 0 |
(3)观察所画的图象,写出该函数的两条性质: .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等腰三角形ABC的底边BC长为6,面积是18,腰AC的垂直平分线EF分别交AC,AB于E,F点,若点D为BC边的中点,点M为线段EF上一动点,则△CDM的周长的最小值为_____.
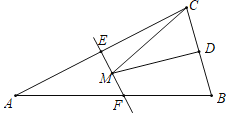
查看答案和解析>>
科目:初中数学 来源: 题型:
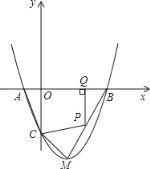
【题目】如图,抛物线y=ax2+bx+c与x轴交于A、B两点(点A在点B左侧),与y轴交于点C,且当x=0和x=2时,y的值相等.直线y=3x﹣7与这条抛物线相交于两点,其中一点的横坐标是4,另一点是这条抛物线的顶点M.
(1)求这条抛物线的解析式;
(2)P为线段BM上一点,过点P向x轴引垂线,垂足为Q.若点P在线段BM上运动(点P不与点B、M重合),设OQ的长为t,四边形PQAC的面积为S.求S与t之间的函数关系式及自变量t的取值范围;
(3)在线段BM上是否存在点N,使△NMC为等腰三角形?若存在,请求出点N的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com