练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    12．如图，在△ABC中，∠C=90°，BD平分∠ABC，交AC于D．若DC=3，则点D到AB的距离是3．

    分析 过点D作DE⊥AB于点E，根据角平分线的性质可知：DE=CD．

    解答 解：过点D作DE⊥AB于点E，
    ∵BD平分∠ABC，
    ∠C=∠BED=90°
    ∴DE=CD=3，
    ∴点D到AB的距离为3，
    故答案为：3

    点评 本题考查角平分线的性质，属于基础题型．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    2．（1）如图1，已知线段a，利用尺规，求作一条线段AB，使AB=2a．
    （2）如图2，已知线段a、b，利用尺规，求作一条线段AB，使AB=a+2b．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    3．我校图书馆上周借书记录如下：（超过100本记为正，少于100本记为负）．
    星期一星期二星期三星期四星期五
    +230-17+6-12
    （1）上星期五借出多少本书？
    （2）上星期四比上星期三多借出多少本书？
    （3）上周平均每天借出图书多少本？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

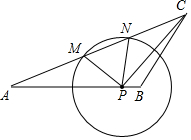    20．如图，已知在△ABC中，AB=15，AC=20，点P在AB边上，⊙P的半径为定长．当点P与点B重合时，⊙P恰好与AC边相切；当点P与点B不重合时，⊙P与AC边相交于点M和点N，且PM：AB=1：$\sqrt{5}$
    （1）求⊙P的半径；
    （2）当AP=6 $\sqrt{5}$时，试探究△APM与△PCN是否相似，并说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

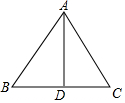    7．如图，已知△ABC中，AB=AC，AD平分∠BAC，请将“等腰三角形三线合一”定理的证明过程补充完整．
    解：∵AD平分∠BAC
    ∴∠BAD=∠CAD（角平分线的定义）
    在△ABD和△ACD中
    AB=AC；
    ∠BAD=∠CAD；
    AD=AD；
    ∴△ABD≌△ACD （SAS）
    ∴BD=DC （全等三角形的对应边相等）
    ∠ADB=∠ADC=$\frac{1}{2}$×180°=90°
    即AD是BC上中线，也是BC上的高．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    17．下列说法中，正确的说法有（　　）
    ①对角线互相平分且相等的四边形是菱形；
    ②一元二次方程x2-3x-4=0的根是x1=4，x2=-1；
    ③依次连结任意四边形各边中点所得的四边形是平行四边形；
    ④一元一次不等式2x+5≤11的整数解有3个；
    ⑤某班演讲比赛，共有甲、乙、丙三位选手，班主任让三位选手抽签决定演讲先后顺序，从先到后恰好是甲、乙、丙的概率是$\frac{1}{3}$．
    A．1个B．2个C．3个D．4个

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    4．如图，在数轴上点A表示的数最可能是（　　）
    A．-2B．-2.5C．-3.5D．-2.9

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    1．观察如图中的几何体，画出从左面、上面两个方向看到的形状图．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

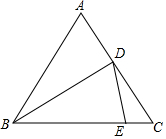    2．如图，边长为2的等边△ABC中，D、E分别为AC、BC上的点（D、E与顶点不重合），∠BDE=60°．
    （1）求证：△ABD∽△CDE；
    （2）设CD=x，BE=y，求y与x的函数关系式，并求y的最小值．

    查看答案和解析>>

    同步练习册答案