
已知一次函数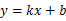 的图象经过点(
的图象经过点(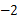 ,
,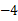 ),且与正比例函数
),且与正比例函数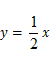 的图象相交于点(4,
的图象相交于点(4,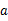 ),
),
求:(1)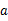 的值;
的值;
(2)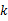 、
、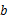 的值;
的值;
(3)求出这两个函数的图象与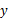 轴相交得到的三角形的面积.
轴相交得到的三角形的面积.
科目:初中数学 来源: 题型:解答题
如图,在平面直角坐标系xOy中,矩形ABCD的边AD=6,A(1,0), B(9,0),直线y=kx+b经过B、D两点.
(1)求直线y=kx+b的表达式;
(2)将直线y=kx+b平移,当它与矩形没有公共点时,直接写出b的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,在直角坐标系xOy中,直线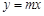 与双曲线
与双曲线 相交于
相交于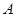 、B
、B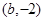 两点,矩形
两点,矩形 的边
的边 恰好被点
恰好被点 平分,边
平分,边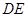 交双曲线于
交双曲线于 点,四边形
点,四边形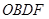 的面积为2.
的面积为2.
(1)求n的值;
(2)求不等式 的解集
的解集
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
某中学为了了解全校的耗电情况,抽查了10天中全校每天的耗电量,数据如下表:
| 千瓦时 | 90 | 93 | 102 | 113 | 114 | 120 |
| 天数 | 1 | 1 | 2 | 3 | 1 | 2 |
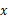 (
(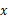 取正整数,单位:天)的函数关系式.
取正整数,单位:天)的函数关系式.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
某车间有甲、乙两条生产线.在甲生产线已生产了200吨成品后,乙生产线开始投入生产,甲、乙两条生产线每天分别生产20吨和30吨成品.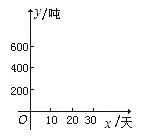
(1)分别求出甲、乙两条生产线各自总产量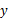 (吨)与从乙开始投产以来所用时间
(吨)与从乙开始投产以来所用时间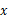 (天)之间的函数关系式.
(天)之间的函数关系式.
(2)作出上述两个函数在如图所示的直角坐标系中的图象,观察图象,分别指出第10天和第30天结束时,哪条生产线的总产量高?
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,直线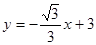 和x轴、y轴的交点分别为B、C,点A的坐标是(
和x轴、y轴的交点分别为B、C,点A的坐标是( ,0),另一条直线经过点A、C.
,0),另一条直线经过点A、C.
(1)求直线AC所对应的函数表达式;
(2)动点M从B出发沿BC运动,运动的速度为每秒1个单位长度.当点M运动到C点时停止运动.设M运动t秒时,△ABM的面积为S.
① 求S与t的函数关系式;
② 当t为何值时,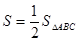 (注:
(注: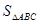 表示△ABC的面积),求出对应的t值;
表示△ABC的面积),求出对应的t值;
③当 t=4的时候,在坐标轴上是否存在点P,使得△BMP是以BM为直角边的直角三角形?若存在,请直接写出P点坐标,若不存在,请说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,在等腰直角三角板ABC中,斜边BC为2个单位长度,现把这块三角板在平面直角坐标系xOy中滑动,并使B、C两点始终分别位于y轴、x轴的正半轴上,直角顶点A与原点O位于BC两侧.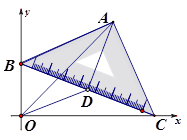
(1)取BC中点D,问OD+DA的长度是否发生改变,若会,说明理由;若不会,求出OD+DA长度;
(2)你认为OA的长度是否会发生变化?若变化,那么OA最长是多少?OA最长时四边形OBAC是怎样的四边形?并说明理由;
(3)填空:当OA最长时A的坐标是( , ),直线OA的解析式是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com