
分析 分别求出各个正多边形和圆的面积,再比较不同图形面积的大小即可.
解答 解:围成圆形场地面积较大.理由如下:
∵正三角形的周长为12m,则边长为4m,
∴正三角形的面积=$\frac{1}{2}$×4×2$\sqrt{3}$=4$\sqrt{3}$(m2)
∵正方形的边长为12m,则边长为3m,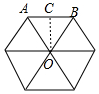
∴正方形的面积=13×3=9(m2);
∵正六边形的周长为12m,则边长AB=12÷6=2(m),
过O作OC⊥AB,如图所示:
∵AB=BO=AO=2,
∴CO=$\sqrt{{2}^{2}-{1}^{2}}$=$\sqrt{3}$,
∴正六边形面积为=$\frac{1}{2}$×2×$\sqrt{3}$×6=6$\sqrt{3}$(m2);
∵2πr=12,∴r=$\frac{6}{π}$,
∴S=πr2=π×$\frac{{6}^{2}}{{π}^{2}}$=$\frac{36}{π}$(m2);
∵4$\sqrt{3}$<9<6$\sqrt{3}$<$\frac{36}{π}$,
∴围成圆形场地面积较大.
点评 此题主要考查了正多边形和圆的性质;熟练掌握正多边形和圆的面积的计算方法是解决问题的关键.


科目:初中数学 来源: 题型:解答题
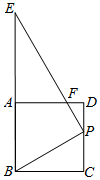 如图,将一个Rt△BPE与正方形ABCD 叠放在一起,并使其直角顶点P落在线段CD上(不与C,D两点重合),斜边的一部分与线段AB重合.
如图,将一个Rt△BPE与正方形ABCD 叠放在一起,并使其直角顶点P落在线段CD上(不与C,D两点重合),斜边的一部分与线段AB重合.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
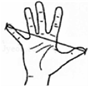 如图,大拇指与小拇指尽量张开时,两指尖的距离称为指距.根据最近人体构造学的研究成果表明,一般情况下人的指距d和身高h成某种关系.如表是测得的指距与身高的一组数据:
如图,大拇指与小拇指尽量张开时,两指尖的距离称为指距.根据最近人体构造学的研究成果表明,一般情况下人的指距d和身高h成某种关系.如表是测得的指距与身高的一组数据:| 指距d(cm) | 20 | 21 | 22 | 23 |
| 身高h(cm) | 160 | 169 | 178 | 187 |
| A. | 25.3厘米 | B. | 26.3厘米 | C. | 27.3厘米 | D. | 28.3厘米 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
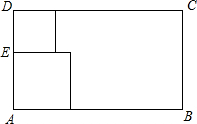 如图所示,从一张矩形纸较短的边上找一点E.过点E剪下两个正方形,它们的边长分别是AE,DE,要使剪下的两个正方形的面积和最小,点E应选在何处?
如图所示,从一张矩形纸较短的边上找一点E.过点E剪下两个正方形,它们的边长分别是AE,DE,要使剪下的两个正方形的面积和最小,点E应选在何处?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
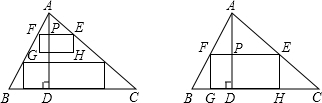 如图,△ABC中,BC=10cm,BC边上的高AD=8cm,E、F分别为AC、AB上的点,且EF∥BC,以EF为边向下作矩形EFGH,且满足EF=2FG,设EF的长为x(cm),矩形EFGH与△ABC重叠部分的面积为y(cm2).
如图,△ABC中,BC=10cm,BC边上的高AD=8cm,E、F分别为AC、AB上的点,且EF∥BC,以EF为边向下作矩形EFGH,且满足EF=2FG,设EF的长为x(cm),矩形EFGH与△ABC重叠部分的面积为y(cm2).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
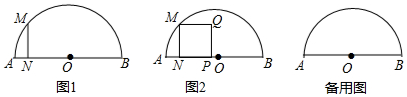
 如图,已知P是两直角边分别为3cm、4cm的Rt△ABC斜边AB上的任意一点,以CP为直径作圆,则该圆的面积y(cm2)与CP的长x(cm)之间的函数关系式是y=$\frac{1}{4}$πx2,自变量x的取值范围是2.4≤x≤4,y的最小值是1.44π,y的最大值是4π.
如图,已知P是两直角边分别为3cm、4cm的Rt△ABC斜边AB上的任意一点,以CP为直径作圆,则该圆的面积y(cm2)与CP的长x(cm)之间的函数关系式是y=$\frac{1}{4}$πx2,自变量x的取值范围是2.4≤x≤4,y的最小值是1.44π,y的最大值是4π.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com