
【题目】已知a,b为有理数,且a,b不为0,则定义有理数对(a,b)的“真诚值”为d(a,b)= ,如有理数对(3,2)的“真诚值”为d(3,2)=23﹣10=﹣2,有理数对(﹣2,5)的“真诚值”为d(﹣2,5)=(﹣2)5﹣10=﹣42.
,如有理数对(3,2)的“真诚值”为d(3,2)=23﹣10=﹣2,有理数对(﹣2,5)的“真诚值”为d(﹣2,5)=(﹣2)5﹣10=﹣42.
(1)求有理数对(﹣3,2)与(1,2)的“真诚值”;
(2)求证:有理数对(a,b)与(b,a)的“真诚值”相等;
(3)若(a,2)的“真诚值”的绝对值为|d(a,2)|,若|d(a,2)|=6,求a的值.
【答案】(1)d(﹣3,2)的“真诚值”为﹣1,d(1,2)的“真诚值”为﹣9;(2)见解析;(3)见解析.
【解析】
(1)根据题目中的新定义,可以求得有理数对(﹣3,2)与(1,2)的“真诚值”;
(2)根据题意分类讨论当a>b时和当a<b时,再结合新定义进行证明结论;
(3)由|d(a,2)|=6,得到d(a,2)=±6,分d(a,2)=6和d(a,2)=﹣6时进行讨论即可得到答案.
(1)d(﹣3,2)=(﹣3)2﹣10=9﹣10=﹣1,d(1,2)=12﹣10=1﹣10=﹣9;
(2)证明:由题知:
ⅰ当a>b时,因为d(a,b)=ba﹣10,d(b,a)=ba﹣10,
所以d(a,b)=d(b,a);
ⅱ当a<b时,因为d(a,b)=ab﹣10,(b,a)=ab﹣10,
所以d(a,b)=d(b,a);
综合所得:d(a,b)=d(b,a);
(3)因为|d(a,2)|=6,所以d(a,2)=±6,
ⅰ、若d(a,2)=6,
当a>2 时,2a﹣10=6,2a=16,得a=4成立;
当a<2 时,a2﹣10=6,a2=16,得a=±4,
因为a<2,所以a=﹣4;
ⅱ、若d(a,2)=﹣6时
当a>2 时,2a﹣10=﹣6,2a=4,得a=2不成立;
当a<2 时,a2﹣10=﹣6,a2=4,得a=±2,
因为a<2,所以a=﹣2;
由上可得,a=﹣2或±4.


 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案科目:初中数学 来源: 题型:
【题目】如图1,二次函数y=ax2+bx的图象过点A(﹣1,3),顶点B的横坐标为1.

(1)求这个二次函数的表达式;
(2)点P在该二次函数的图象上,点Q在x轴上,若以A、B、P、Q为顶点的四边形是平行四边形,求点P的坐标;
(3)如图3,一次函数y=kx(k>0)的图象与该二次函数的图象交于O、C两点,点T为该二次函数图象上位于直线OC下方的动点,过点T作直线TM⊥OC,垂足为点M,且M在线段OC上(不与O、C重合),过点T作直线TN∥y轴交OC于点N.若在点T运动的过程中, ![]() 为常数,试确定k的值.
为常数,试确定k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:数a,b,c 在数轴上的对应点如下图所示,
(1)在数轴上表示﹣a;
(2)比较大小(填“<”或“>”或“=”):a+b 0,﹣3c 0,c﹣a 0;
(3)化简|a+b|﹣|﹣3c|﹣|c﹣a|.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,D为AB边上一点,E为CD中点,AC=![]() ,∠ABC=30°,∠A=∠BED=45°,则BD的长为( )
,∠ABC=30°,∠A=∠BED=45°,则BD的长为( )

A. ![]() B.
B. ![]() +1﹣
+1﹣![]() C.
C. ![]() ﹣
﹣![]() D.
D. ![]() ﹣1
﹣1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,数轴上每相邻两点的相距一个单位长度,点A、B、C、D是这些点中的四个,且对应的位置如图所示,它们对应的数分别是a,b,c,d.
(1)当ab=﹣1,则d= .
(2)若|d﹣2a|=7,求点C对应的数.
(3)若abcd<0,a+b>0,化简|a﹣b|﹣|b+c﹣5|﹣|c﹣5|﹣|d﹣a|+|8﹣d|.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有三个有理数x,y,z,若x=![]() ,且x与y互为相反数,y是z的倒数.
,且x与y互为相反数,y是z的倒数.
(1)当n为奇数时,你能求出x,y,z这三个数吗?当n为偶数时,你能求出x,y,z,这三个数吗?若能,请计算并写出结果;若不能,请说明理由.
(2)根据(1)的结果计算:xy﹣yn﹣(y﹣z)2019的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,甲、乙两块边长为a米(a>1)的正方形田地,甲地修了两条互相垂直的宽为1米的通道,乙地正中间修了边长为1米的蓄水池,甲乙两田地的剩余地方全部种植小麦,一年后收获小麦m千克.(m>0)

(1)甲地的小麦种植面积为 平方米,乙地的小麦种植面积为 平方米;
(2)甲乙两地小麦种植面积较小的是 地;
(3)若高的单位面积产量是低的单位面积产量的![]() 倍,求a的值.
倍,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列方程变形中,正确的是( )
A.方程3x-2=2x+1,移项,得3x-2x=1-2
B.方程3-x=2-5(x-1),去括号,得3-x=2-5x-1;
C.方程-75x=76,方程两边同除以-75,得x=-![]()
D.方程![]() =1+
=1+![]() ,去分母,得2(2x-1)=6+3(x-3)
,去分母,得2(2x-1)=6+3(x-3)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,矩形ABCD中,AE平分![]() 交BC于E,
交BC于E,![]() ,则下面的结论:①
,则下面的结论:①![]() 是等边三角形;②
是等边三角形;②![]() ;③
;③![]() ;④
;④![]() ,其中正确结论有( )
,其中正确结论有( )
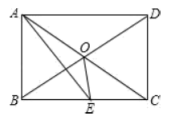
A. 1个B. 2个C. 3个D. 4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com