
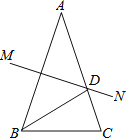
【题目】如图,AB=AC,AB的垂直平分线MN交AC于点D,若∠A=36°,则下列结论:①∠C=72°;②BD是∠ABC的平分线;③△ADB是等腰三角形;④△BCD的周长=AB+BC.正确是______(填序号).
【答案】①②③④
【解析】
①,△ABC中,∠A=36°,AB=AC,根据等腰三角形的性质与三角形内角和定理,即可求得∠C的度数;
对于②,分别求出∠ABD与∠DBC的度数,便可判断BD是否是∠ABC的平分线;
对于③,由线段垂直平分线的性质,得到AD=BD,即可判断△ABD的形状;
对于④,由AD=BD,AC=AB,根据三角形的周长周长公式及线段间的等量代换即可得△BCD的周长.
∵ AB=AC,
∴ ∠ABC=∠ACB.
∵ ∠BAC=36°,
∴ ∠ABC=∠ACB=72° .
故①正确;
∵ MN垂直平分AB,
∴ AD=BD,
∴ △ABD是等腰三角形,
∴ ∠BAC=∠ABD=36° .
∵ ∠ABD=36°,∠ABC=72°,
∴ ∠DBC=36°,
∴ BD平分∠ABC.
故②③正确;
∵ AD=BD,
∴ △BCD的周长=BD+CD+BC=AD+DC+BC=AC+BC.
∵ AC=AB,
∴ △BCD的周长=AB+BC.
故④正确.
综上可知,结论中成立的有①②③④.


 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案科目:初中数学 来源: 题型:
【题目】如图①所示是一个长为2m,宽为2n的长方形,沿图中虚线用剪刀均分成四个小长方形,然后按图②的方式拼成一个正方形.

(1)你认为图②中的阴影部分的正方形的边长等于_________________;
(2)请用两种不同的方法列代数式表示图②中阴影部分的面积.
方法① __________________.方法② _____________________;
(3)观察图②,你能写出(m+n)2,(m-n)2,mn这三个代数式之间的等量关系吗?
答:________________________ .
(4)根据(3)题中的等量关系,解决如下问题:若a+b=6,ab=4,则求(a-b)2的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校组织九年级学生参加汉字听写大赛,并随机抽取部分学生成绩作为样本进行分析,绘制成如下的统计表:


请根据所给信息,解答下列问题:
(1)a=__________,b=__________;
(2)请补全频数分布直方图;
(3)已知该年级有400名学生参加这次比赛,若成绩在90分以上(含90分)的为优,估计该年级成绩为优的有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
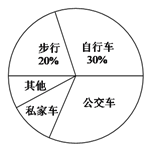
【题目】某校为了解全校2400名学生到校上学的方式,在全校随机抽取了若干名学生进行问卷调查.问卷给出了五种上学方式供学生选择,每人只能选一项,且不能不选.将调查得到的结果绘制成如图所示的频数分布直方图和扇形统计图(均不完整).
(1)这次调查中,一共抽取了多少名学生?
(2)补全频数分布直方图;
(3)估计全校所有学生中有多少人乘坐公交车上学.

查看答案和解析>>
科目:初中数学 来源: 题型:
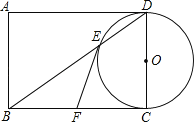
【题目】如图,以矩形ABCD的边CD为直径作⊙O,交矩形的对角线BD于点E,点F是BC的中点,连接EF.
(1)试判断EF与⊙O的位置关系,并说明理由.
(2)若DC=2,EF=![]() ,点P是⊙O上不与E、C重合的任意一点,则∠EPC的度数为 (直接写出答案)
,点P是⊙O上不与E、C重合的任意一点,则∠EPC的度数为 (直接写出答案)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在ABCD中,对角线AC,BD相交于点0,添加下列条件后,能使ABCD成为矩形的是( )
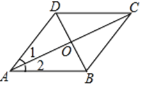
A. AB=ADB. AC=BDC. BD平分∠ABCD. AC⊥BD
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把一个含45°角的直角三角尺BEF和个正方形ABCD摆放在起,使三角尺的直角顶点和正方形的顶点B重合,连接DF,DE,M,N分别为DF,EF的中点,连接MA,MN,下列结论错误的是( )
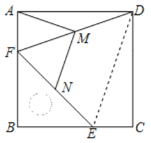
A. ∠ADF=∠CDEB. △DEF为等边三角形
C. AM=MND. AM⊥MN
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】张明、王成两位同学在初二学年10次数学单元检测的成绩(成绩均为整数,且个位数为0)如图所示利用图中提供的信息,解答下列问题:
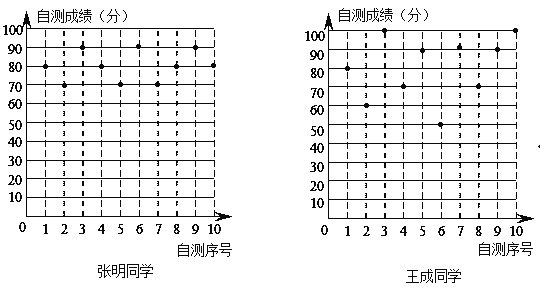
(1)完成下表:
姓名 | 平均成绩 | 中位数 | 众数 | 方差(s2) |
张明 |
| 80 | 80 |
|
王成 |
|
|
| 260 |
(2)如果将90分以上(含90分)的成绩视为优秀,则优秀率较高的同学是 ;
(3)根据图表信息,请你对这两位同学各提出学习建议.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A,B的坐标分别为A(0,a),B(b,a),且a,b满足(a﹣3)2+|b﹣6|=0.现将线段AB向下平移3个单位,再向左平移2个单位,得到线段CD,点A,B的对应点分别为点C,D.连接AC,BD.
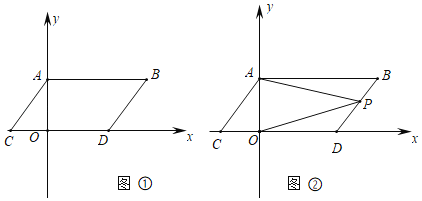
(1)如图①,求点C,D的坐标及四边形ABDC的面积;
(2)在y轴上是否存在一点M,使三角形MCD的面积与四边形ABDC的面积相等?若存在,求出点M的坐标,若不存在,试说明理由;
(3)如图②,点P是直线BD上的一个动点,连接PA,PO,当点P在直线BD上移动时(不与B,D重合),直接写出∠BAP,∠DOP,∠APO之间满足的数量关系.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com