

分析 (1)根据等腰三角形的性质得到∠ACD=∠D,∠BCE=∠E,由三角形的内角和得到∠CAB+∠CBA=100°,根据三角形的外角的性质得到∠CDA+∠BCE=$\frac{1}{2}$(∠CAB+∠CBA)=50°,即可得到结论;
(2)根据三角形的内角和和外角的性质即可得到结论;
(3)点D、E分别在直线AB上,除去(1)(2)两种情况,还有两种情况,如图3,由(1)知,∠D=$\frac{1}{2}∠$CAB,由(2)知∠CEB=$\frac{180°-∠B}{2}$,列方程即可求得结果.
(4)在△ABC中,AB=14,AC=15,BC=13,过C作CF⊥AB与F,根据勾股定理求得AB边上的高CF=12,然后根据三角形的面积公式即可强大的结论.
解答  解:(1)∵AD=AC,BE=BC,
解:(1)∵AD=AC,BE=BC,
∴∠ACD=∠D,∠BCE=∠E,
∵∠ACB=80°,
∴∠CAB+∠CBA=100°,
∴∠CDA+∠BCE=$\frac{1}{2}$(∠CAB+∠CBA)=50°,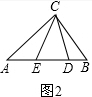
∴∠DCE=130°,
故答案为:130°.
(2)∵∠ACB=80°,
∴∠A+∠B=100°,
∵AD=AC,BE=BC,
∴∠ACD=∠ADC,∠BEC=∠BCE,
∴∠ADC=$\frac{180-∠A}{2}$,∠BEC=$\frac{180-∠B}{2}$,
∴∠ADC+∠BEC=180°-$\frac{1}{2}$(∠A+∠B)=130°,
∴∠DCE=50°;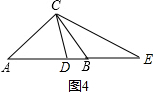
(3)点D、E分别在直线AB上,除去(1)(2)两种情况,还有两种情况,如图3,
由(1)知,∠D=$\frac{1}{2}∠$CAB,由(2)知∠CEB=$\frac{180°-∠B}{2}$,
∴∠CEB=∠D+∠DCE,
∴$\frac{180°-∠B}{2}$=$\frac{1}{2}∠$CAB+∠DCE,
∴∠DCE=40°,
如图4,同理∠DCE=40°;
(4)在△ABC中,AB=14,AC=15,BC=13,
过C作CF⊥AB与F,
则AC2-AF2=BC2-BF2,即152-AF2=132-(14-AF)2,
解得:AF=9,
∴CF=12,
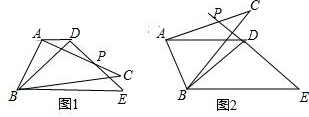
①如图1,DE=AB+AC+BC=42,
∴S△CDE=$\frac{1}{2}$×42×12=252;
②如图2,DE=AC+BC-AB=14,
∴S△CDE=$\frac{1}{2}$×14×12=84;
③如图3,DE=AC+AB-BC=16,
∴S△CDE=$\frac{1}{2}$×16×12=96;
④如图4,DE=AB+BC-AC=12,
∴S△CDE=$\frac{1}{2}$×12×12=72.
点评 本题考查了等腰三角形的性质,勾股定理,三角形的面积,熟练掌握等腰三角形的性质是解题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 人数 | 1日 | 2日 | 3日 | 4日 | 5日 | 6日 | 7日 |
| 人数变化 | +1.6 | +0.8 | +0.4 | -0.4 | -0.8 | +0.2 | -1.2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 9日 | 10日 | 11日 | |
| 购进(千克) | 50 | 48 | 52 |
| 售出(千克) | 42 | 49 | 46 |
| 损耗(千克) | 4 | 2 | 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com