
分析 (1)设L1的“友好抛物线”的表达式为:y=-x2+bx,根据L1:y=x2-2x可得其顶点坐标,代入y=-x2+bx可得b的值,进而得出L1的“友好抛物线”;
(2)先求出抛物线L1和L2的顶点坐标,根据L2过L1 的顶点,得出bn=0,进而得到抛物线L1经过L2的顶点,再根据L2与L1的开口大小相同,方向相反,即可得出抛物线L1也是L2的“友好抛物线”;
(3)根据“友好抛物线”的定义,得到m=-a,进而得到L2的顶点为($\frac{n}{2a}$,$\frac{{n}^{2}}{4a}$).根据抛物线L2的顶点在第一象限,纵坐标为2,可得a=$\frac{1}{8}$n2>0.再根据L2经过点P(1,0),得到a=8.根据L2经过点Q(3,0),得到a=$\frac{8}{9}$.进而得出抛物线L2与线段PQ没有公共点时,a的取值范围.
解答 解:(1)依题意,可设L1的“友好抛物线”的表达式为:y=-x2+bx,
∵L1:y=x2-2x=(x-1)2-1,
∴L1的顶点为(1,-1),
∵y=-x2+bx过点(1,-1),
∴-1=-12+b,即b=0.
∴L1的“友好抛物线”为:y=-x2.
(2)L2:y=mx2+nx的顶点为(-$\frac{n}{2m}$,-$\frac{{n}^{2}}{4m}$),L1:y=ax2+bx的顶点为(-$\frac{b}{2a}$,-$\frac{{b}^{2}}{4a}$),
∵L2为L1 的“友好抛物线”,
∴m=-a.
∵L2过L1 的顶点,
∴-$\frac{{b}^{2}}{4a}$=m×(-$\frac{b}{2a}$)2+n×(-$\frac{b}{2a}$).
化简得:bn=0.
把x=-$\frac{n}{2m}$代入y=ax2+bx,得
y═a×(-$\frac{n}{2m}$)2+b×(-$\frac{n}{2m}$)=-$\frac{{n}^{2}}{4m}$-$\frac{bn}{2m}$=-$\frac{{n}^{2}}{4m}$.
∴抛物线L1经过L2的顶点.
又∵L2与L1的开口大小相同,方向相反,
∴抛物线L1也是L2的“友好抛物线”.
(3)∵抛物线L2:y=mx2+nx为L1:y=ax2的“友好抛物线”,
∴m=-a.
∴L2:y=-ax2+nx的顶点为($\frac{n}{2a}$,$\frac{{n}^{2}}{4a}$).
∵抛物线L2的顶点在第一象限,纵坐标为2,
∴$\frac{{n}^{2}}{4a}$=2,即a=$\frac{1}{8}$n2>0.
当L2经过点P(1,0)时,-a+n=0,
∴a=8.
当L2经过点Q(3,0)时,-9a+3n=0,
∴a=$\frac{8}{9}$.
∴抛物线L2与线段PQ没有公共点时,0<a<$\frac{8}{9}$或a>8.
点评 本题属于二次函数综合题,主要考查了二次函数的图象与性质的运用,解题时根据给定的函数或函数图象判断出系数的符号,然后判断新的函数关系式中系数的符号,再根据系数与图象的位置关系判断出图象特征.解这类问题关键是善于将函数问题转化为方程问题,善于利用几何图形的有关性质、定理和二次函数的知识,并注意挖掘题目中的一些隐含条件.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
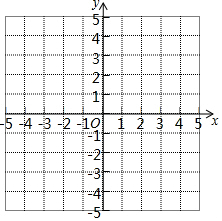 (1)在同一坐标系中画出一次函数y=x-1,y=2x-3图象;
(1)在同一坐标系中画出一次函数y=x-1,y=2x-3图象;查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com