
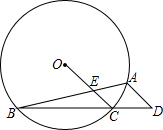
已知:如图,⊙O的内接△ABC中,∠BAC=45°,∠ABC=15°,AD∥OC并交BC的延长线于D,OC交AB于E.
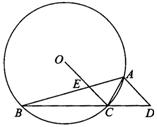
1.求∠D的度数;
2.求证:AC2=AD·CE;
3.求![]() 的值.
的值.
1.解:如图,连结OB.

∵⊙O的内接△ABC中,∠BAC=45°,
∴∠BOC=2∠BAC=90°.
∵OB=OC,
∴∠OBC=∠OCB=45°.
∵AD∥OC,
∴∠D=∠OCB=45°.
2.证明:∵∠BAC=45°,∠D=45°,
∴∠BAC=∠D.
∵AD∥OC,
∴∠ACE=∠DAC.
∴△ACE∽△DAC.

∴AC2=AD·CE.
3.解法一:如图,延长BO交DA的延长线于F,连结OA.
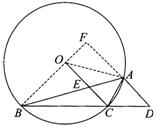
∵AD∥OC,
∴∠F=∠BOC=90°.
∵∠ABC=15°,
∴∠OBA=∠OBC-∠ABC=30°.
∵OA=OB.
∴∠FOA=∠OBA+∠OAB=60°,∠OAF=30°.
∴![]() .
.
∵AD∥OC,
∴△BOC∽△BFD.
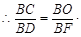
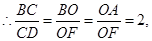 即
即![]() 的值为2.
的值为2.
解法二:作OM⊥BA于M,设⊙O的半径为r,可得![]()
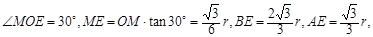
所以![]()
解析:略


科目:初中数学 来源: 题型:
 OC交AB于E.
OC交AB于E.| BC | CD |
查看答案和解析>>
科目:初中数学 来源:2011-2012学年北京市九年级上学期期中考试数学卷 题型:解答题
已知:如图,⊙O的内接△ABC中,∠BAC=45°,∠ABC =15°,AD∥OC并交BC的延长线于D,OC交AB于E。

1.(1)求∠D的度数;
2.(2)求证: ;
;
3.(3)求 的值。
的值。
查看答案和解析>>
科目:初中数学 来源:2012届北京市西城区九年级下学期期末检测数学卷 题型:解答题
已知:如图,⊙O的内接△ABC中,∠BAC=45°,∠ABC=15°,AD∥OC并交BC的延长线于D,OC交AB于E.

1.求∠D的度数;
2.求证:AC2=AD·CE;
3.求 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com