(1)解:当∠CDF=60°时,如图2,
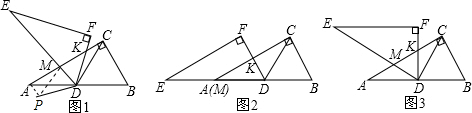
∵∠ACB=∠F=90°,∠CAD=30°,D为AB的中点,
∴DC=DA=DB,
∴∠KCD=30°,
∴∠CKD=90°,
∴KA=KC,
而AM=0,
∴m=
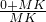
=1;
当∠CDF=30°时,如图3,
∴KC=KD,∠MKD=30°+30°=60°,
∵∠MDK=60°,
∴△DMK为等边三角形,
∴MK=KD=MD,∠KMD=60°,
∵∠A=30°,
∴∠MDA=∠KMD-∠A=30°,
∴MA=MD,
∴MA=MK=KC,
∴m=
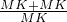
=2;
(2)证明:作∠ADP=α,DP=DK,如图1,
∵在△ADP和△CDK中,
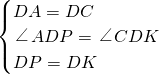
,
∴△ADP≌△CDK(SAS),
∴AP=CK,
∵∠ADC=120°,∠MDK=60°,
∴∠ADM=120°-60°-α=60°-α,
∴∠MDP=60°-α+α=60°,
∵在△MDP和△MDK中,
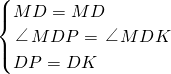
,
∴△MDP≌△MDK(SAS),
∴PM=MK,
∵AM+AP>PM,
∴AM+KC>MK,
∴m>1;
(3)解:如图1,由(2)得PM=MK,AP=CK,
∵MK
2+CK
2=AM
2,
∴PM
2+AP
2=AM
2,
∴∠APM=90°,
∵∠MAD=30°,∠DAP=∠DCK=30°,
∴∠MAP=60°,
∴∠AMP=30°,
∴AM=2AP,MP=

AP,
∴AM=2CK,MP=

CK,
∴m=
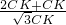
=

;
∵△MDP≌△MDK,
∴∠KMD=∠PMD=
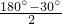
=75°,
∴∠MKD=180°-75°-60°=45°,
而∠MKD=∠KCD+∠CDK,
∴∠CDK=45°-30°=15°,即∠CDF=15°.
故答案为1,2;15;

.
分析:(1)先根据直角三角形斜边上的中线性质得到△CDA是等腰三角形,再由∠CAD=30°,∠CDF=60°得到∠CKD=90°,则KA=KC,然后计算m的值;当∠CDF=30°时,
可得到KC=KD,∠MKD=30°+30°=60°,得到△DMK为等边三角形,所以MK=KD=MD,∠KMD=60°,再证出MD=MA,然后计算m的值;
(2)作∠ADP=α,DP=DK,则根据“SAS”得到△ADP≌△CDK,得到AP=CK,再计算出∠MDP=60°,则可根据“SAS”可得△MDP≌△MDK,则PM=MK,根据三角形三边的关系得到AM+AP>PM,即AM+KC>MK,于是可得到m>1;
(3)由(2)得PM=MK,AP=CK,由MK
2+CK
2=AM
2得到PM
2+AP
2=AM
2,根据勾股定理的逆定理得∠APM=90°,由∠MAD=30°,∠DAP=∠DCK=30°可得∠MAP=60°,然后根据含30°的直角三角形三边的关系得到AM=2AP,MP=

AP,即AM=2CK,MP=

CK,则可计算出m的值;接着计算出∠KMD=∠PMD=75°,∠MKD=45°,然后利用三角形外角性质可计算出α的度数.
点评:本题考查了全等三角形的判定与性质:判定三角形全等的方法有“SSS”、“SAS”、“ASA”、“AAS”;全等三角形的对应边相等.也考查了等边三角形的判定与性质、含30°的直角三角形三边的关系以及勾股定理的逆定理.

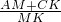 =m.
=m.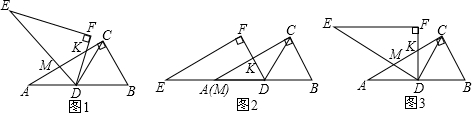

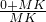 =1;
=1;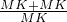 =2;
=2;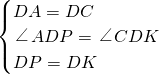 ,
,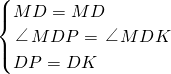 ,
, AP,
AP, CK,
CK,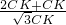 =
= ;
;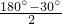 =75°,
=75°, .
. AP,即AM=2CK,MP=
AP,即AM=2CK,MP= CK,则可计算出m的值;接着计算出∠KMD=∠PMD=75°,∠MKD=45°,然后利用三角形外角性质可计算出α的度数.
CK,则可计算出m的值;接着计算出∠KMD=∠PMD=75°,∠MKD=45°,然后利用三角形外角性质可计算出α的度数.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 (2012•和平区二模)如图,在Rt△ABC中,∠BAC=90°,AB=6,AM为∠BAC的平分线,CM=2BM.下列结论:
(2012•和平区二模)如图,在Rt△ABC中,∠BAC=90°,AB=6,AM为∠BAC的平分线,CM=2BM.下列结论: (2013•遵义)如图,在Rt△ABC中,∠ACB=90°,AC=BC=1,E为BC边上的一点,以A为圆心,AE为半径的圆弧交AB于点D,交AC的延长于点F,若图中两个阴影部分的面积相等,则AF的长为
(2013•遵义)如图,在Rt△ABC中,∠ACB=90°,AC=BC=1,E为BC边上的一点,以A为圆心,AE为半径的圆弧交AB于点D,交AC的延长于点F,若图中两个阴影部分的面积相等,则AF的长为 的外接圆.
的外接圆. (2013•嘉定区二模)如图,在Rt△ABC中,∠ACB=90°,点D在AC边上,且BC2=CD•CA.
(2013•嘉定区二模)如图,在Rt△ABC中,∠ACB=90°,点D在AC边上,且BC2=CD•CA.