
【题目】如图,对称轴为x=1的抛物线经过A(﹣1,0),B(4,5)两点.
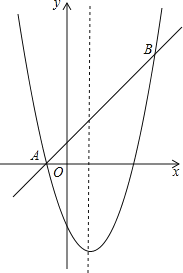
(1)求抛物线的解析式;
(2)P为直线AB上的动点,过点P作x轴的垂线交抛物线于点Q.
①当PQ=6时,求点P的坐标;
②是否存在点P,使以A、P、Q为顶点的三角形为等腰三角形?若存在,直接写出点P的坐标;若不存在,请说明理由.
【答案】(1)y=x2﹣2x﹣3;(2)①当PQ=6时,点P的坐标(1,2),(2,3),(﹣2,﹣1),(5,6);②存在点P,使以A、P、Q为顶点的三角形为等腰三角形,点P的坐标为P(4+![]() ,5+
,5+![]() )或(4﹣
)或(4﹣![]() ,5﹣
,5﹣![]() )或(4,5)或(3.4).
)或(4,5)或(3.4).
【解析】
试题分析:(1)根据题意确定抛物线与x轴的另一个交点,然后根据待定系数法即可求得;
(2)①先求得直线AB的解析式,设P(m,m+1),Q(m,m2﹣2m﹣3),则PQ=|m+1﹣m2+2m+3|=6,然后分m2﹣3m﹣4=﹣6或m2﹣3m﹣4=6两种情况求得m的值,从而求得P点的坐标;
②由勾股定理,得PA2=(m+1)2+(m+1)2;PQ2=[m+1﹣(m2﹣2m﹣3)]2,AQ2=(m+1)2+(m2﹣2m﹣3)2.然后分PA=PQ、PA=AQ、AQ=AP三种情况列出关于m的方程,解方程求得m的值,即可求得P点的坐标.
解:(1)对称轴为x=1的抛物线经过A(﹣1,0),得C(3,0),
设抛物线的解析式为y=ax2+bx+c,将A、B、C点坐标代入,得
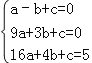 ,
,
解得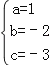 ,
,
设抛物线的解析式为y=x2﹣2x﹣3;
(2)①直线AB的解析式为y=x+1,设P(m,m+1),Q(m,m2﹣2m﹣3),
PQ=|m+1﹣m2+2m+3|=6,
当m2﹣3m﹣4=﹣6,
解得m=1,m=2,
∴P(1,2)或(2,3);
当m2﹣3m﹣4=6,解得m=﹣2,m=5,
∴P(﹣2,﹣1)或(5,6);
综上所述:当PQ=6时,点P的坐标(1,2),(2,3),(﹣2,﹣1),(5,6);
(3)∵A(﹣1,0),P(m,m+1),Q(m,m2﹣2m﹣3),由勾股定理,得
PA2=(m+1)2+(m+1)2;PQ2=[m+1﹣(m2﹣2m﹣3)]2,AQ2=(m+1)2+(m2﹣2m﹣3)2.
①当PA=PQ时,(m+1)2+(m+1)2=[m+1﹣(m2﹣2m﹣3)]2,化简,得(m+1)2[(m﹣4)2﹣2]=0.
于是,得(m﹣4)2﹣2=0,m+1=0.
解得m1=4+![]() ,m2=4﹣
,m2=4﹣![]() ,m3=﹣1,
,m3=﹣1,
∵当m=﹣1时,P点与A点重合,
∴P1(4+![]() ,5+
,5+![]() ),P2(4﹣
),P2(4﹣![]() ,5﹣
,5﹣![]() );
);
②当PA=AQ时,(m+1)2+(m+1)2=(m+1)2+(m2﹣2m﹣3)2,化简,得(m+1)2(m﹣3﹣1)2=0,
于是,得(m﹣4)2=0,解得m4=4,m5=﹣1,
∴P3(4,5);
③当AQ=AP时,(m+1)2+(m2﹣2m﹣3)2=[m+1﹣(m2﹣2m﹣3)]2,化简,得(m+1)2[(m﹣4)2﹣2]=0.
于是,得(m2﹣2m﹣3)2=0.m+1=0,
解得m6=3,m7=﹣1,
∴P(3,4);
综上,存在点P,使以A、P、Q为顶点的三角形为等腰三角形,点P的坐标为P(4+![]() ,5+
,5+![]() )或(4﹣
)或(4﹣![]() ,5﹣
,5﹣![]() )或(4,5)或(3.4).
)或(4,5)或(3.4).


科目:初中数学 来源: 题型:
【题目】甲布袋中有三个红球,分别标有数字1,2,3;乙布袋中有三个白球,分别标有数字2,3,4.这些球除颜色和数字外完全相同.小亮从甲袋中随机摸出一个红球,小刚从乙袋中随机摸出一个白球.
(1)用画树状图(树形图)或列表的方法,求摸出的两个球上的数字之和为6的概率;
(2)小亮和小刚做游戏,规则是:若摸出的两个球上的数字之和为奇数,小亮胜;否则,小刚胜.你认为这个游戏公平吗?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
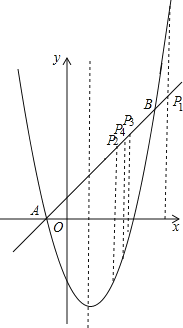
【题目】如图,是抛物线y=ax2+bx+c(a≠0)图象的一部分.已知抛物线的对称轴为x=2,与x轴的一个交点是(﹣1,0).有下列结论:
①abc>0;
②4a﹣2b+c<0;
③4a+b=0;
④抛物线与x轴的另一个交点是(5,0);
⑤点(﹣3,y1),(6,y2)都在抛物线上,则有y1<y2.
其中正确的是( )
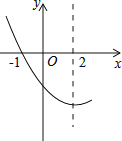
A.①②③ B.②④⑤ C.①③④ D.③④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
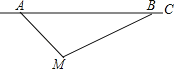
【题目】根据道路管理规定,在贺州某段笔直公路上行驶的车辆,限速40千米/时,已知交警测速点M到该公路A点的距离为10![]() 米,∠MAB=45°,∠MBA=30°(如图所示),现有一辆汽车由A往B方向匀速行驶,测得此车从A点行驶到B点所用的时间为3秒.
米,∠MAB=45°,∠MBA=30°(如图所示),现有一辆汽车由A往B方向匀速行驶,测得此车从A点行驶到B点所用的时间为3秒.
(1)求测速点M到该公路的距离;
(2)通过计算判断此车是否超速.(参考数据:![]() ≈1.41,
≈1.41,![]() ≈1.73,
≈1.73,![]() ≈2.24)
≈2.24)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在正方形ABCD中,DE为正方形的外角∠ADF的角平分线,点G在线段AD上,过点G作PG⊥DE于点P,连接CP,过点D作DQ⊥PC于点Q,交射线PG于点H.
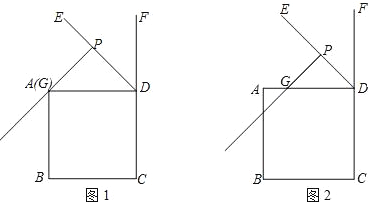
(1)如图1,若点G与点A重合.
①依题意补全图1;
②判断DH与PC的数量关系并加以证明;
(2)如图2,若点H恰好在线段AB上,正方形ABCD的边长为1,请写出求DP长的思路(可以不写出计算结果).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com