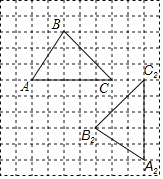
【题目】如图，在边长为1个单位长度的小正方形组成的网格中，△ABC为格点三角形（顶点在网格线的交点）．
（1）将△ABC向上平移2个单位得到△A1B1C1，请画出△A1B1C1；
（2）将△ABC绕着某点O逆时针方向旋转90°后，得到△A2B2C2，请画出旋转中心O，并直接写出在此旋转过程中，线段AB扫过的区域的面积．
天天向上一本好卷系列答案
小学生10分钟应用题系列答案科目：初中数学 来源： 题型：
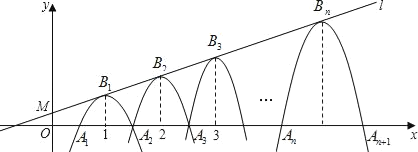
【题目】定义：若抛物线的顶点与x轴的两个交点构成的三角形是直角三角形，则这种抛物线被称为：“直角抛物线”．如图，直线l：y＝
x+b经过点M(0，
)，一组抛物线的顶点B1(1，y1)，B2(2，y2)，B3(3，y3)，…Bn(n，yn) (n为正整数)，依次是直线l上的点，第一个抛物线与x轴正半轴的交点A1(x1，0)和A2(x2，0)，第二个抛物线与x轴交点A2(x2，0)和A3(x3，0)，以此类推，若x1＝d(0＜d＜1)，当d为_____时，这组抛物线中存在直角抛物线．
查看答案和解析>>
科目：初中数学 来源： 题型：
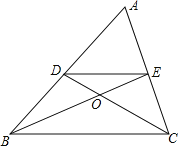
【题目】如图，在△ABC中，D、E分别是AB、AC的中点，BE交CD于点O，连接DE，有下列结论：①DE＝
BC；②△BOC∽△COE；③BO＝2EO；④AO的延长线经过BC的中点．其中正确的是____．（填写所有正确结论的编号）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知抛物线y＝mx2﹣4mx+3m（m＞0）与x轴的交点为A，B，与y轴的交点为C，D为抛物线的顶点．
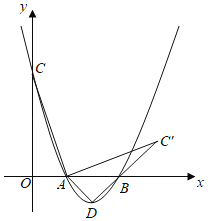
（1）直接写出各点坐标C（ ， ），D（ ， ）；（用m表示）
（2）试说明无论m为何值，抛物线一定经过两个定点并求出这两个定点的坐标；
（3）①将线段AC绕点A顺时针旋转90°得到AC′，求点C′的坐标；
②连接DC'，AD，是否存在m，使得△ADC′为等腰三角形？若存在，请求出m；若不存在，请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在边长为12的正方形
中，对角线
、
交于点
，点
、
分别为
、
边上的动点，且始终保持
，连接
交于点
.
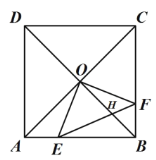
(1)求证：
；
(2)若
，求
的值；
(3)在运动的过程中，是否存在最大值？若存在，请求出的最大值；若不存在，请说明理由.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】（已知：如图所示的一张矩形纸片ABCD（AD>AB），将纸片折叠一次，使点A与点C重合，再展开，折痕EF交AD边于点E，交BC边于点F，分别连结AF和CE．
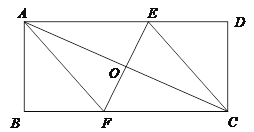
（1）求证：四边形AFCE是菱形；
（2）若AE=10cm，△ABF的面积为24cm2，求△ABF的周长；
（3）在线段AC上是否存在一点P，使得2AE2=AC·AP？若存在，请说明点P的位置，并予以证明；若不存在，请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
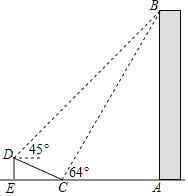
【题目】如图，在大楼AB的正前方有一斜坡CD，CD=13米，坡比DE:EC=1： 
，高为DE，在斜坡下的点C处测得楼顶B的仰角为64°，在斜坡上的点D处测得楼顶B的仰角为45°，其中A、C、E在同一直线上．
（1）求斜坡CD的高度DE；
（2）求大楼AB的高度；（参考数据：sin64°≈0.9，tan64°≈2）．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在△ABC中，D、E分别是AB、BC上的点，且DE∥AC，若S△BDE：S△CDE=1：4，则S△BDE：S△DAC=（ ）
A.1：25B.1：20C.1：18D.1：16
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
