
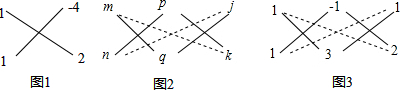
分析 (1)①直接用十字相乘法分解因式;②把某个字母看成常数用十字相乘法分解即可;③同②的方法分解;
(2)用十字相乘法把能分解的集中情况全部列出求出m值.
解答 解:(1)①6x2-17xy+12y2=(3x-4y)(2x-3y),
②2x2-xy-6y2+2x+17y-12=(x-2y+3)(2x+3y-4),
③x2-xy-6y2+2x-6y=(x-3y)(x+2y+2),
故答案为:①(3x-4y)(2x-3y),②(x-2y+3)(2x+3y-4),③(x-3y)(x+2y+2),
(2)如图,
m=3×9+(-8)×(-2)=43
或m=9×(-8)+3×(-2)=-78.
点评 此题是因式分解-十字相乘法,主要考查了二元二次多项式的分解因式的方法,解本题的关键是选好那个字母当做常数对待,再用十字相乘法分解.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
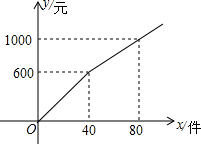 商户小李以每件6元的价格购进某商品若干件到市场去销售,销售金额y(元)与销售量x(件)的函数关系的图象如图所示,则降价后每件商品销售的价格为( )
商户小李以每件6元的价格购进某商品若干件到市场去销售,销售金额y(元)与销售量x(件)的函数关系的图象如图所示,则降价后每件商品销售的价格为( )| A. | 5元 | B. | 10元 | C. | 12.5元 | D. | 15元 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com