练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    当x≠-1时，对于分式
    1
    x-1
    总有（　　）
    分析：根据分式的基本性质：分式的分子分母同时乘以（x+1），x≠-1，则x+1≠0可得答案．
    解答：解：
    1
    x-1
    =
    1•(x+1)
    (x-1)(x+1)
    =
    x+1
    x2-1
    ．
    故选：B．
    点评：此题主要考查了分式的基本性质，关键是注意分式的分子分母必须同时乘以同一个不为零的数．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    19、对于一元二次方程x2+bx+c=0，下列说法正确的序号是
    ①②④
    ．（多填或错填得0分，少填酌情给分）
    ①当c=0时，则方程必有一根为零；
    ②当c＜0时，则方程必有两个不相等的实数根；
    ③当c＞0，b=0时，则方程两根互为相反数；
    ④当c＞0，b＞0，b2＞4c时，则方程的两根必为负数

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    已知点A（-1，0），点B（与A不重合）在射线AO上，点C在x轴上方，且△ABC为等边三角形，射线AC交y轴于D．
    （1）当AB=4时，则点B、C、D的坐标分别是：B：
    （3，0）
    （3，0）
    ，C：
    （1，2
    		3
    ）
    （1，2
    		3
    ）
    ，D：
    （0，
    		3
    ）
    （0，
    		3
    ）
    ；
    （2）若AB=m（m＞0），则点B、C的坐标分别是：B：
    （m-1，0）
    （m-1，0）
    ，C：
    （
    1
    2
    m-1，
    		3
    2
    m）
    （
    1
    2
    m-1，
    		3
    2
    m）
    ；
    当C、D不重合时，请根据m的不同取值，对于过B、C、D三点的二次函数开口方向作出判断，直接写出结论（不要求证明）．
    （3）是否存在点B，使S△BCD=
    3
    		3
    16
    ？若存在，求出点B的坐标；若不存在，请说明理由．

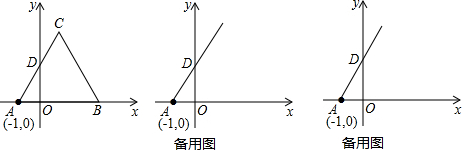
    查看答案和解析>>

    科目：初中数学 来源： 题型：

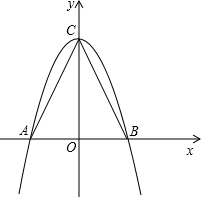    （2012•柳州）如图，在△ABC中，AB=2，AC=BC=
    		5
    ．
    （1）以AB所在的直线为x轴，AB的垂直平分线为y轴，建立直角坐标系如图，请你分别写出A、B、C三点的坐标；
    （2）求过A、B、C三点且以C为顶点的抛物线的解析式；
    （3）若D为抛物线上的一动点，当D点坐标为何值时，S△ABD=
    1
    2
    S△ABC；
    （4）如果将（2）中的抛物线向右平移，且与x轴交于点A′B′，与y轴交于点C′，当平移多少个单位时，点C′同时在以A′B′为直径的圆上（解答过程如果有需要时，请参看阅读材料）．
     
    附：阅读材料
    一元二次方程常用的解法有配方法、公式法和因式分解法，对于一些特殊方程可以通过换元法转化为一元二次方程求解．如解方程：y4-4y2+3=0．
    解：令y2=x（x≥0），则原方程变为x2-4x+3=0，解得x1=1，x2=3．
    当x1=1时，即y2=1，∴y1=1，y2=-1．
    当x2=3，即y2=3，∴y3=
    		3
    ，y4=-
    		3
    ．
    所以，原方程的解是y1=1，y2=-1，y3=
    		3
    ，y4=-
    		3
    ．
    再如x2-2=4
    		x2-2
    ，可设y=
    		x2-2
    ，用同样的方法也可求解．

    查看答案和解析>>

    科目：初中数学 来源：2010-2011学年江苏省仪征市大仪中学七年级下学期期中考试数学卷 题型：解答题

    (本题10分)
    我们用“☆”、“★”定义新运算：对于任意有理数数，，都有☆＝2×2，★＝2÷2，例如：3☆2＝23×22＝25=32，3★2＝23÷22＝2.
    (1)求4018★（2011☆2009）的值.
    (2)当为何值时，(2)☆1的值与2010★2003的值相等.

    查看答案和解析>>

    科目：初中数学 来源：2013届江苏省仪征市七年级下学期期中考试数学卷 题型：解答题

    (本题10分)

    我们用“☆”、“★”定义新运算：对于任意有理数数，，都有☆＝2×2，★＝2÷2，例如：3☆2＝23×22＝25=32，3★2＝23÷22＝2.

    (1)求4018★（2011☆2009）的值.

    (2)当为何值时，(2)☆1的值与2010★2003的值相等.

     

    查看答案和解析>>

    同步练习册答案