
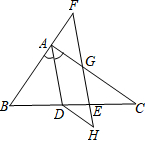
 如图,AD平分∠BAC,点F在BA的延长线上,点E在线段CD上,EF与AC相交于点G,且∠BDA=180°-∠CEG.
如图,AD平分∠BAC,点F在BA的延长线上,点E在线段CD上,EF与AC相交于点G,且∠BDA=180°-∠CEG.分析 (1)根据∠ADB+∠CEG=180°,∠ADB+∠ADE=180°,可得∠ADE=∠CEG,进而判定AD∥EF;
(2)先推出HD∥AC,根据平行线的性质得出∠H=∠CGH,再根据平行线的性质得到∠CAD=∠CGH,∠BAD=∠F,进而得到∠H=∠CAD,根据角平分线定义得出∠BAD=∠CAD,即可得到∠F与∠H相等.
解答 解:(1)AD∥EF.
理由:∵∠ADB+∠CEG=180°,∠ADB+∠ADE=180°,
∴∠ADE=∠CEG,
∴AD∥EF;
(2)∠F=∠H,
理由:∵∠EDH=∠C,
∴HD∥AC,
∴∠H=∠CGH,
∵AD∥EF,
∴∠CAD=∠CGH,∠BAD=∠F,
∴∠H=∠CAD,
∵AD平分∠BAC,
∴∠BAD=∠CAD,
∴∠H=∠F.
点评 本题考查了平行线的性质和判定,解题时注意:平行线的判定是由角的数量关系判断两直线的位置关系,平行线的性质是由平行关系来寻找角的数量关系.


科目:初中数学 来源: 题型:解答题
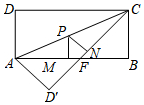 如图,矩形ABCD中,AB=8,BC=4,将△ADC沿AC折叠,点D落在点D′处,CD′与AB交于点F.
如图,矩形ABCD中,AB=8,BC=4,将△ADC沿AC折叠,点D落在点D′处,CD′与AB交于点F.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
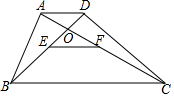 四边形ABCD中,AD∥BC,AC交BD于O,AD=5,BC=9,E,F分别是BD、AC的中点,下列结论正确的有①②④(填序号).
四边形ABCD中,AD∥BC,AC交BD于O,AD=5,BC=9,E,F分别是BD、AC的中点,下列结论正确的有①②④(填序号).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 小张对他所在学校的同学使用手机的情况进行了调查,并根据调查的结果制作了如图所示的统计图,由图可知,利用手机玩游戏的同学占30%,则利用手机上网学习的同学所在的扇形的圆心角的度数是72°.
小张对他所在学校的同学使用手机的情况进行了调查,并根据调查的结果制作了如图所示的统计图,由图可知,利用手机玩游戏的同学占30%,则利用手机上网学习的同学所在的扇形的圆心角的度数是72°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
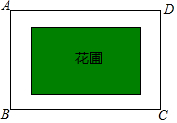 如图,学校计划在一块长为60米,宽为40米的长方形空地ABCD内修建一个长方形花圃,并将花圃四周余下的空地修建成同样宽的通道,设通道宽为a米.
如图,学校计划在一块长为60米,宽为40米的长方形空地ABCD内修建一个长方形花圃,并将花圃四周余下的空地修建成同样宽的通道,设通道宽为a米.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com