
【题目】已知:∠MON=36°,OE平分∠MON,点A,B分别是射线OM,OE,上的动点(A,B不与点O重合),点D是线段OB上的动点,连接AD并延长交射线ON于点C,设∠OAC=x,
(1)如图1,若AB∥ON,则
①∠ABO的度数是______;
②当∠BAD=∠ABD时,x=______;
当∠BAD=∠BDA时,x=______;
(2)如图2,若AB⊥OM,则是否存在这样的x的值,使得△ABD中有两个相等的角?若存在,求出x的值;若不存在,请说明理由.

【答案】(1)①18°;②126°;③63°;(2)当x=18、36、54时,△ADB中有两个相等的角.
【解析】
(1)运用平行线的性质以及角平分线的定义,可得∠ABO的度数;根据∠ABO、∠BAD的度数以及△AOB的内角和,可得x的值;
(2)根据三角形内角和定理以及直角的度数,可得x的值.
解:(1)如图1,①∵∠MON=36°,OE平分∠MON,
∴∠AOB=∠BON=18°,
∵AB∥ON,
∴∠ABO=18°;
②当∠BAD=∠ABD时,∠BAD=18°,
∵∠AOB+∠ABO+∠OAB=180°,
∴∠OAC=180°-18°×3=126°;
③当∠BAD=∠BDA时,∵∠ABO=18°,
∴∠BAD=81°,∠AOB=18°,
∵∠AOB+∠ABO+∠OAB=180°,
∴∠OAC=180°-18°-18°-81°=63°,
故答案为①18°;②126°;③63°;
(2)如图2,存在这样的x的值,使得△ADB中有两个相等的角.
∵AB⊥OM,∠MON=36°,OE平分∠MON,
∴∠AOB=18°,∠ABO=72°,
若∠BAD=∠ABD=72°,则∠OAC=90°-72°=18°;
若∠BAD=∠BDA=(180°-72°)÷2=54°,则∠OAC=90°-54°=36°;
若∠ADB=∠ABD=72°,则∠BAD=36°,故∠OAC=90°-36°=54°;
综上所述,当x=18、36、54时,△ADB中有两个相等的角.


 学业测评一课一测系列答案
学业测评一课一测系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,以AC为直径作⊙O交BC于点D,交AB于点G,且D是BC中点,DE⊥AB,垂足为E,交AC的延长线于点F.
(1)求证:直线EF是⊙O的切线;
(2)若CF=3,cosA=0.4,求出⊙O的半径和BE的长;
(3)连接CG,在(2)的条件下,求CG:EF的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某城市规定:出租车起步价允许行驶的最远路程为3千米,超过3千米的部分按每千米另行收费,甲说:“我乘这种出租车走了11千米,付了17元”;乙说:“我乘这种出租车走了23千米,付了35元”.请你算一算这种出租车的起步价是多少元?以及超过3千米后,每千米的车费是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为加快“秀美荆河水系生态治理工程”进度,污水处理厂决定购买10台污水处理设备.现有A,B两种型号的设备,每台的价格分别为a万元,b万元,每月处理污水量分别为240吨,200吨.已知购买一台A型设备比购买一台B型设备多2万元,购买2台A型设备比购买3台B型设备少6万元.
(1)求a,b的值;
(2)厂里预算购买污水处理设备的资金不超过105万元,你认为有哪几种购买方案;
(3)在(2)的条件下,若每月要求处理污水量不低于2040吨,为了节约资金,请你为污水处理厂设计一种最省钱的购买方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
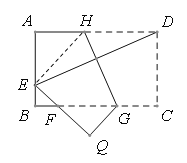
【题目】如图,将矩形ABCD沿GH对折,点C落在Q处,点D落在AB边上E处,EQ与BC相交于F,若AD=8 cm,AB=6 cm,AE=4cm,则△EBF的周长是______________ cm.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com