
【题目】如图1,△ABC中,∠B=30°,点D在BA的延长线上,点E在BC边上,连接DE,交AC于点F.若∠EFC=60°,DE=2AC,求![]() 的值.某学习小组的同学经过思考,交流了自己的想法:
的值.某学习小组的同学经过思考,交流了自己的想法:
小明:“通过观察和度量,发现∠C与∠D存在某种数量关系”;
小强:“通过构造三角形,证明三角形相似,进而可以求得![]() 的值.
的值.
老师:如图2,将原题中“点D在BA的延长线上,点E在BC边上”改为“点D在AB边上,点E在BC的延长线上”,添加条件“BC=5![]() ,EC=4
,EC=4![]() ”,其它条件不变,可求出△BED的面积.
”,其它条件不变,可求出△BED的面积.
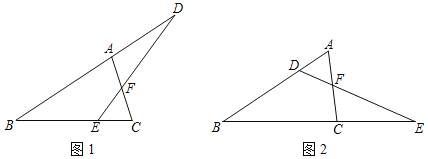
请回答:
(1)用等式表示∠C、∠D的数量关系并证明;
(2)求![]() 的值;
的值;
(3)△BDE的面积为 (直接写出答案).
【答案】(1)∠C+∠D=90°,见解析;(2)![]() ;(3)18
;(3)18![]()
【解析】
(1)结论:∠C+∠D=90°.利用三角形的内角和定理解决问题即可.
(2)过点A作AG⊥BC垂足为G,交DE点Q,过点E作EH⊥BD垂足为H,则∠DHE=∠BHE=90°.利用相似三角形的性质解决问题即可.
(3)如图2中,在BA上取一点G,使得GB=GC,作GJ⊥BC于J,AH⊥CG于H,EK⊥BA交BA的延长线于K.利用相似三角形的性质解决问题即可.
解:(1)结论:∠C+∠D=90°.
理由:如图1中,
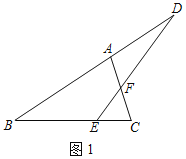
∵∠AFD=∠EFC=60°,
∵∠BAC=180°﹣∠C﹣30°=150°﹣∠C,∠BAC=∠AFD+∠D=60°+∠D,
∴150°﹣∠C=60°+∠D,
∴∠C+∠D=90°.
(2)过点A作AG⊥BC垂足为G,交DE点Q,过点E作EH⊥BD垂足为H,则∠DHE=∠BHE=90°.
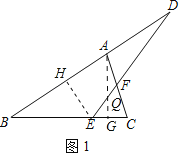
∵∠AGC=90°,
∴∠DHE═∠AGC.
∵∠C+∠D=90°, ∠C+∠CAG=90°.
∴∠D=∠CAG,
∴△DEH∽△ACG.
∴![]() .
.
∴DH=2AG.
∵∠B=30°,∠AGB=90°,
∴AB=2AG.
∴AB=DH.
∴AB﹣AH=DH﹣AH.
即BH=AD.
在Rt△BHE中,![]() =cos30°=
=cos30°=![]() .
.
∴![]() =
=![]() =
=![]() .
.
(3)如图2中,在BA上取一点G,使得GB=GC,作GJ⊥BC于J,AH⊥CG于H,EK⊥BA交BA的延长线于K.

∵∠BAC=180°﹣∠B﹣∠ACB=180°﹣∠ADE﹣∠AFD,
∴150°﹣∠ACB=120°﹣∠ADF,
∴∠ACB﹣30°=∠ADE,
∵GB=GC,GJ⊥BC,
∴∠GCB=∠B=30°,BJ=JC=![]() =
=![]() ,
,
∴∠ACH=∠ACB﹣30°=∠EDK,BG=CG=![]() =5,
=5,
∵∠ACH=∠EDK,∠AHC=∠K=90°,
∴△DEK∽△CAH,
∴![]() ,
,
在Rt△BKE中,∵∠K=90°,∠B=30°,BE=9![]() ,
,
∴EK=![]() ,BK=
,BK=![]() ,
,
∴AH=![]() ,
,
∴GH=![]() AH=
AH=![]() ,
,
∴CH=CG﹣GH=![]() ,
,
∴DK=2CH=![]() ,
,
∴BD=BK﹣DK=![]() ﹣
﹣![]() =8,
=8,
∴S△BDE=![]() BD·EK=
BD·EK=![]() ×8×
×8×![]() =18
=18![]() .
.
故答案为18![]() .
.


 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案科目:初中数学 来源: 题型:
【题目】如图,小宋作出了边长为2的第一个正方形A1B1C1D1,算出了它的面积.然后分别取正方形A1B1C1D1四边的中点A2、B2、C2、D2作出了第二个正方形A2B2C2D2,算出了它的面积.用同样的方法,作出了第三个正方形A3B3C3D3,算出了它的面积…,由此可得,第六个正方形A6B6C6D6的面积是( )
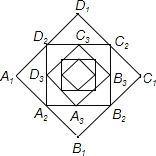
A.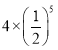 B.
B.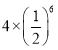 C.
C.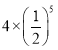 D.
D.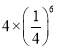
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学选拔一名青年志愿者:经笔试、面试,结果小明和小丽并列第一.评委会决定通过抓球来确定人选.规则如下:在不透明的布袋里装有除颜色之外均相同的2个红球和1个绿球,小明先取出一个球,记住颜色后放回,然后小丽再取出一个球.若两次取出的球都是红球,则小明胜出;若两次取出的球是一红一绿,则小丽胜出.你认为这个规则对双方公平吗?请用列表法或画树状图的方法进行分析.
查看答案和解析>>
科目:初中数学 来源: 题型:
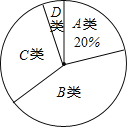
【题目】某校为了解本校九年级男生“引体向上”项目的训练情况,随机抽取该年级部分男生进行了一次测试(满分15分,成绩均记为整数分),按测试成绩m(单位:分)分为A、B、C、D四个组别并绘制出以下两幅不完整的统计图,请根据图中信息解答下列问题:
(1)在被调查的男生中,成绩等级为D的男生有 人,成绩等级为A的男生人数占被调查男生人数的百分比为 %;
(2)本次抽取样本容量为 ,成绩等级为C的男生有 人;
(3)若该校九年级男生有300名,估计成绩少于9分的男生人数.
分组 | 成绩 | 人数 |
A | 12≤m≤15 | 10 |
B | 9≤m≤11 | 22 |
C | 6≤m≤8 | |
D | m≤5 | 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
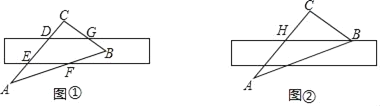
【题目】将直尺摆放在三角板上,使直尺与三角板的边分别交于点D、E、F、G,如图①所示.已知∠CGD=42.
(1)求∠CEF的度数.
(2)将直尺向下平移,使直尺的边缘通过点B,交AC于点H,如图②所示.点H、B的读数分别为4、13.4,求BC的长(精确到0.1)(参考数据:sin42°=0.67,cos42°=0.74,tan42°=0.90)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形网格中的每个小正方形的边长都是1,每个小正方形的顶点叫做格点.△ABC的三个顶点A,B,C都在格点上.将△ABC绕点A按顺时针方向旋转90°得到△AB′C′.
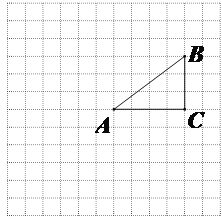
(1)在正方形网格中,画出△AB′C′;
(2)计算线段AB在变换到AB′的过程中扫过的区域的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,对角线AC与BD交于点O.过点C作BD的平行线,过点D作AC的平行线,两直线相交于点E.
(1)求证:四边形OCED是矩形;
(2)若CE=1,DE=2,ABCD的面积是 .

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com