
【题目】找出图中所有的同位角、内错角、同旁内角.

【答案】图1中的同位角:∠1与∠8,∠2与∠5,∠3与∠6,∠4与∠7,内错角有∠1与∠6,∠4与∠5;同旁内角有∠1与∠5,∠4与∠6;图2同位角有∠1与∠3,∠2与∠4,同旁内角有∠2与∠3.
【解析】
根据同位角就是:两个角都在截线的同旁,又分别处在被截的两条直线同侧的位置的角,内错角是两个角都在截线的两侧,又分别处在被截的两条直线中间的位置的角,同旁内角是两个角都在截线的同旁,又分别处在被截的两条直线中间位置的角,可得答案.
如图:
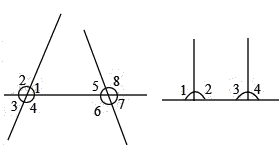
图1中的同位角:∠1与∠8,∠2与∠5,∠3与∠6,∠4与∠7,
内错角有∠1与∠6,∠4与∠5;
同旁内角有∠1与∠5,∠4与∠6;
图2同位角有∠1与∠3,∠2与∠4,
同旁内角有∠2与∠3.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】某种型号油电混合动力汽车,从A地到B地燃油行驶纯燃油费用76元,从A地到B地用电行驶纯电费用26元,已知每行驶1千米,纯燃油费用比纯用电费用多0.5元.
(1)求每行驶1千米纯用电的费用;
(2)若要使从A地到B地油电混合行驶所需的油、电费用合计不超过39元,则至少用电行驶多少千米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知三角形纸片ABC的面积为48,BC的长为8.按下列步骤将三角形纸片ABC进行裁剪和拼图:
第一步:如图1,沿三角形ABC的中位线DE将纸片剪成两部分.在线段DE上任意取一点F,在线段BC上任意取一点H,沿FH将四边形纸片DBCE剪成两部分;
第二步:如图2,将FH左侧纸片绕点D旋转180°,使线段DB与DA重合;将FH右侧纸片绕点E旋转180°,使线段EC与EA重合,再与三角形纸片ADE拼成一个与三角形纸片ABC面积相等的四边形纸片.


图1 图2
(1)当点F,H在如图2所示的位置时,请按照第二步的要求,在图2中补全拼接成的四边形;
(2)在按以上步骤拼成的所有四边形纸片中,其周长的最小值为_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC内接于⊙O , AC是⊙O的直径,D是弧AB的中点.过点D作CB的垂线,分别交CB、CA延长线于点F、E . 
(1)判断直线EF与⊙O的位置关系,并说明理由;
(2)若CF=6,∠ACB=60°,求阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直线y=kx+b经过A(0,2),B(4,0)两点.
(1)求直线AB对应的函数解析式;
(2)将该直线向上平移6个单位,求平移后的直线与x轴交点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行于x轴的直线AC分别交抛物线y1=x2(x≥0)与y2= ![]() (x≥0)于B、C两点,过点C作y轴的平行线交y1于点D,直线DE∥AC,交y2于点E,则
(x≥0)于B、C两点,过点C作y轴的平行线交y1于点D,直线DE∥AC,交y2于点E,则 ![]() = .
= . 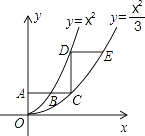
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示的图案是由六个全等的直角三角形组成,点O是该图案的中心,则该图案可看成由一个直角三角形绕O点顺时针依次旋转________得到,或可看成由两个相邻的直角三角形绕O点顺时针依次旋转________得到,或可看成由三个相邻的直角三角形绕O点旋转________得到.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中国式过马路,是网友对部分中国人集体闯红灯现象的一种调侃,即“凑够一撮人就可以走了,和红绿灯无关”针对这种现象某媒体记者在多个路口采访闯红灯的行人,得出形成这种现象的四个基本原因:①红绿灯设置不科学,交通管理混乱;②侥幸心态;③执法力度不够;④从众心理.该记者将这次调查情况整理并绘制了如下尚不完整的统计图,请根据相关信息,解答下列问题. 
(1)该记者本次一共调査了名行人;
(2)求图1中④所在扇形的圆心角,并补全图2;
(3)在本次调查中,记者随机采访其中的一名行人,求他属于第②种情况的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com