
【题目】小王电子产品专柜以20元/副的价格批发了某新款耳机,在试销的60天内整理出了销售数据如下
销售数据(第x天) | 售价(元) | 日销售量(副) |
1≤x<35 | x+30 | 100﹣2x |
35≤x≤60 | 70 | 100﹣2x |
(1)若试销阶段每天的利润为W元,求出W与x的函数关系式;
(2)请问在试销阶段的哪一天销售利润W可以达到最大值?最大值为多少?
【答案】(1)见解析;(2)在试销阶段的第20天时W最大,最大值为1800元.
【解析】
(1)利用总利润=单件利润×销量写出函数关系式即可;
(2)配方后确定两个最值,取最大的即可.
解:(1)①当1≤x<35时,W1=(x+30﹣20)(100﹣2x)
即W1=﹣2(x﹣20)2+1800;
②当35≤2x≤26时,W2=(70﹣20)(100﹣2x)
即W2=﹣100x+5000;
故W与x之间的函数关系式为:
W=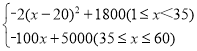 ;
;
(2)∵W1=﹣2(x﹣20)2+1800(1≤x<35),
∴在试销的第一阶段,在第20天时,利润最大为1800元,
∵W2=﹣100x+5000(35≤x≤60),
∴在试销的第二阶段,在第35天时,销售利润最大为1500元,
答:在试销阶段的第20天时W最大,最大值为1800元.


 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案科目:初中数学 来源: 题型:
【题目】受“新冠”疫情的影响,某销售商在网上销售![]() 、
、![]() 两种型号的“手写板”,获利颇丰.已知
两种型号的“手写板”,获利颇丰.已知![]() 型,
型,![]() 型手写板进价、售价和每日销量如表格所示:
型手写板进价、售价和每日销量如表格所示:
进价(元/个) | 售价(元/个) | 销量(个/日) | |
|
|
|
|
|
|
|
|
根据市场行情,该销售商对![]() 型手写板降价销售,同时对
型手写板降价销售,同时对![]() 型手写板提高售价,此时发现
型手写板提高售价,此时发现![]() 型手写板每降低
型手写板每降低![]() 元就可多卖
元就可多卖![]() 个,
个,![]() 型手写板每提高
型手写板每提高![]() 元就少卖
元就少卖![]() 个,要保持每天销售总量不变,设其中
个,要保持每天销售总量不变,设其中![]() 型手写板每天多销售
型手写板每天多销售![]() 个,每天总获利的利润为
个,每天总获利的利润为![]() 元
元
(1)求![]() 与
与![]() 之间的函数关系式并写出
之间的函数关系式并写出![]() 的取值范围;
的取值范围;
(2)要使每天的利润不低于![]() 元,直接写出
元,直接写出![]() 的取值范围;
的取值范围;
(3)该销售商决定每销售一个![]() 型手写板,就捐
型手写板,就捐![]() 元给
元给![]() 因“新冠疫情”影响的困难家庭,当
因“新冠疫情”影响的困难家庭,当![]() 时,每天的最大利润为
时,每天的最大利润为![]() 元,求
元,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现有四个外观与质地完全相同的小球,小球上分别标有数字![]() .将四个小球放置于不透明的盒子中,摇匀后,甲从中随机抽取一个小球,记录数字后放回摇匀,乙再随机抽取一个.
.将四个小球放置于不透明的盒子中,摇匀后,甲从中随机抽取一个小球,记录数字后放回摇匀,乙再随机抽取一个.
(1)请用列表法或画树状图的方法,求两人抽取相同数字的概率.
(2)若两人抽取的数字和为![]() 的倍数,则甲获胜;若抽取的数字和为
的倍数,则甲获胜;若抽取的数字和为![]() 的倍数,则乙获胜,否则为平局.这个游戏公平吗?请用所学的概率的知识加以解释.
的倍数,则乙获胜,否则为平局.这个游戏公平吗?请用所学的概率的知识加以解释.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年某市为创评“全国文明城市”称号,周末团市委组织志愿者进行宣传活动.班主任梁老师决定从4名女班干部(小悦、小惠、小艳和小倩)中通过抽签的方式确定2名女生去参加.
抽签规则:将4名女班干部姓名分别写在4张完全相同的卡片正面,把四张卡片背面朝上,洗匀后放在桌面上,梁老师先从中随机抽取一张卡片,记下姓名,再从剩余的3张卡片中随机抽取第二张,记下姓名.
(1)该班男生“小刚被抽中”是 事件,“小悦被抽中”是 事件(填“不可能”或“必然”或“随机”);第一次抽取卡片“小悦被抽中”的概率为 ;
(2)试用画树状图或列表的方法表示这次抽签所有可能的结果,并求出“小惠被抽中”的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:点P是△ABC内部或边上的点(顶点除外),在△PAB,△PBC,△PCA中,若至少有一个三角形与△ABC相似,则称点P是△ABC的自相似点.
例如:如图1,点P在△ABC的内部,∠PBC=∠A,∠PCB=∠ABC,则△BCP∽△ABC,故点P为△ABC的自相似点.
请你运用所学知识,结合上述材料,解决下列问题:
在平面直角坐标系中,点M是曲线C:![]()
![]() 上的任意一点,点N是x轴正半轴上的任意一点.
上的任意一点,点N是x轴正半轴上的任意一点.
(1) 如图2,点P是OM上一点,∠ONP=∠M, 试说明点P是△MON的自相似点; 当点M的坐标是![]() ,点N的坐标是
,点N的坐标是![]() 时,求点P 的坐标;
时,求点P 的坐标;
(2) 如图3,当点M的坐标是![]() ,点N的坐标是
,点N的坐标是![]() 时,求△MON的自相似点的坐标;
时,求△MON的自相似点的坐标;
(3) 是否存在点M和点N,使△MON无自相似点,?若存在,请直接写出这两点的坐标;若不存在,请说明理由.



查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的顶点A(1,1),B(3,1),规定把正方形ABCD“先沿x轴翻折,再向左平移1个单位”为一次变换,这样连续经过2019次变换后,正方形ABCD的顶点C的坐标为( )
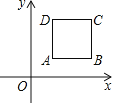
A. (﹣2018,3)B. (﹣2018,﹣3)
C. (﹣2016,3)D. (﹣2016,﹣3)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为建设最美恩施,一旅游投资公司拟定在某景区用茶花和月季打造一片人工花海,经市场调查,购买![]() 株茶花与
株茶花与![]() 株月季的费用相同,购买
株月季的费用相同,购买![]() 株茶花与
株茶花与![]() 株月季共需
株月季共需![]() 元.
元.
(1)求茶花和月季的销售单价;
(2)该景区至少需要茶花月季共![]() 株,要求茶花比月季多
株,要求茶花比月季多![]() 株,但订购两种花的总费用不超过
株,但订购两种花的总费用不超过![]() 元,该旅游投资公司怎样购买所需总费用最低,最低费用是多少.
元,该旅游投资公司怎样购买所需总费用最低,最低费用是多少.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:△ABC中,点D在边AC上,且AB2=ADAC.
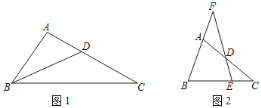
(1)如图1.求证:∠ABD=∠C.
(2)如图2.在边BC上截取BE=BD,ED、BA的延长线交于点F,求证:![]() .
.
(3)在 (2)的条件下,若AD=4,CD=5,cos∠BAC=![]() ,试直接写出△FBE的面积.
,试直接写出△FBE的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
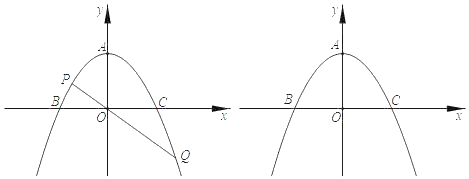
【题目】已知:如图,抛物线![]() 的顶点为A(0,2),与x轴交于B(﹣2,0)、C(2,0)两点.
的顶点为A(0,2),与x轴交于B(﹣2,0)、C(2,0)两点.
(1)求抛物线![]() 的函数表达式;
的函数表达式;
(2)设点P是抛物线y上的一个动点,连接PO并延长至点Q,使OQ=2OP.若点Q正好落在该抛物线上,求点P的坐标;
(3)设点P是抛物线y上的一个动点,连接PO并延长至点Q,使OQ=mOP(m为常数);
①证明点Q一定落在抛物线![]() 上;
上;
②设有一个边长为m+1的正方形(其中m>3),它的一组对边垂直于x轴,另一组对边垂直于y轴,并且该正方形四个顶点正好落在抛物线![]() 和
和![]() 组成的封闭图形上,求线段PQ被该正方形的两条边截得线段长最大时点Q的坐标.
组成的封闭图形上,求线段PQ被该正方形的两条边截得线段长最大时点Q的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com