

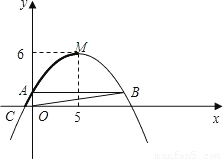
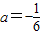 ,则所求抛物线的解析式为
,则所求抛物线的解析式为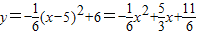 ;
;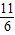 ,结合AB∥x轴,OA⊥AB的性质可知点P到AB的距离为
,结合AB∥x轴,OA⊥AB的性质可知点P到AB的距离为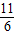 ,设点P的坐标为
,设点P的坐标为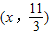 或(x,0),①将
或(x,0),①将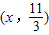 代入
代入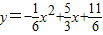 ,解得
,解得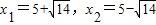
 ,解得x3=-1,x4=11,综合可知点P的坐标为
,解得x3=-1,x4=11,综合可知点P的坐标为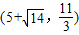 、
、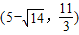 、(-1,0)、(11,0).
、(-1,0)、(11,0). (2分)
(2分) (1分);
(1分); ,
,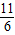 (1分)
(1分)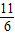 (2分)
(2分)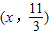 或(x,0)
或(x,0)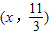 代入
代入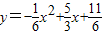 ,
,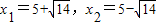 (2分)
(2分)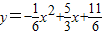 ,
,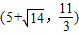 、
、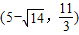 、(-1,0)、(11,0)(1分);
、(-1,0)、(11,0)(1分);

科目:初中数学 来源: 题型:
 (2009•南平)如图,在△ABC中,∠ACB=90°,∠A=30°,将△ABC绕点C顺时针旋转得到△A′B′C,点B′在AB上,A′B′交AC于F,则图中与△AB'F相似的三角形有(不再添加其它线段)( )
(2009•南平)如图,在△ABC中,∠ACB=90°,∠A=30°,将△ABC绕点C顺时针旋转得到△A′B′C,点B′在AB上,A′B′交AC于F,则图中与△AB'F相似的三角形有(不再添加其它线段)( )查看答案和解析>>
科目:初中数学 来源:2009年全国中考数学试题汇编《二次函数》(07)(解析版) 题型:解答题
查看答案和解析>>
科目:初中数学 来源:2011年江苏省泰州市兴化市文正学校中考数学模拟试卷(解析版) 题型:选择题
查看答案和解析>>
科目:初中数学 来源:2009年福建省南平市中考数学试卷(解析版) 题型:选择题





查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com