
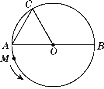
【题目】如图,在⊙O中,AB为⊙O的直径,AC是弦,OC=4,∠OAC=60°.
(1)求∠AOC的度数;
(2)如图,一动点M从A点出发,在⊙O上按逆时针方向运动,当S△MAO=S△CAO时,求动点M所经过的弧长.
【答案】(1)∠AOC=60°;(2)当S△MAO=S△CAO时,动点M所经过的弧长为![]() π或
π或![]() π或
π或![]() π或
π或![]() π.
π.
【解析】
(1)根据等腰三角形中有一角为60度时是等边三角形得到△ACO是等边三角形,即可得到结论;
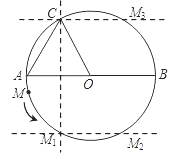
(3)如图,当S△MAO=S△CAO时,动点M的位置有四种.
①作点C关于直径AB的对称点M1,连接AM1,OM1;②过点M1作M1M2∥AB交⊙O于点M2,连接AM2,OM2;③过点C作CM3∥AB交⊙O于点M3,连接AM3,OM3;④当点M运动到C时,M与C重合,求得每种情况的OM转过的度数,再根据弧长公式求得弧AM的长.
(1)在△ACO中,∵∠OAC=60°,OC=OA,∴△ACO是等边三角形,∴∠AOC=60°.
(2)如图,分四种情况讨论:
①作点C关于直径AB的对称点M1,连接AM1,OM1.
易得:S△M1AO=S△CAO,∠AOM1=60°,∴![]() ,∴当点M运动到M1时,S△MAO=S△CAO,此时点M经过的弧长为
,∴当点M运动到M1时,S△MAO=S△CAO,此时点M经过的弧长为![]() .
.
②过点M1作M1M2∥AB交⊙O于点M2,连接AM2,OM2,易得:![]() =S△CAO,∴∠AOM1=∠M1OM2=∠BOM2=60°,∴
=S△CAO,∴∠AOM1=∠M1OM2=∠BOM2=60°,∴![]() 或
或![]() ,∴当点M运动到M2时,S△MAO=S△CAO,此时点M经过的弧长为
,∴当点M运动到M2时,S△MAO=S△CAO,此时点M经过的弧长为![]() .
.
③过点C作CM3∥AB交⊙O于点M3,连接AM3,OM3,易得:![]() =S△CAO,∴∠BOM3=60°,∴
=S△CAO,∴∠BOM3=60°,∴![]() 或
或![]() ,∴当点M运动到M3时,S△MAO=S△CAO,此时点M经过的弧长为
,∴当点M运动到M3时,S△MAO=S△CAO,此时点M经过的弧长为![]() .
.
④当点M运动到C时,M与C重合,S△MAO=S△CAO,此时点M经过的弧长为![]() 或
或![]() .
.
综上所述:当S△MAO=S△CAO时,动点M所经过的弧长为![]() π或
π或![]() π或
π或![]() π或
π或![]() π.
π.


科目:初中数学 来源: 题型:
【题目】八年级(1)班研究性学习小组为研究全校同学课外阅读情况,在全校随机邀请了部分同学参与问卷调查,统计同学们一个月阅读课外书的数量,并绘制了以下统计图.

请根据图中信息解决下列问题:
(1)共有多少名同学参与问卷调查;
(2)补全条形统计图和扇形统计图;
(3)全校共有学生1500人,请估计该校学生一个月阅读2本课外书的人数约为多少.
查看答案和解析>>
科目:初中数学 来源: 题型:
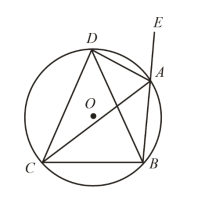
【题目】如图,AD 是△ABC 外角∠EAC 的平分线,AD 与△ABC 的外接圆⊙O 交于点 D.
(1)求证:DB=DC;
(2)若∠CAB=30°,BC=4,求劣弧 CD 的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
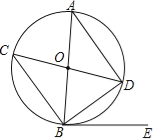
【题目】如图,在⊙O中,AB,CD是直径,BE是切线,B为切点,连接AD,BC,BD.
(1)求证:△ABD≌△CDB;
(2)若∠DBE=37°,求∠ADC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
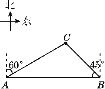
【题目】已知A,B两地相距1 km.要在A,B两地之间修建一条笔直的水渠(即图中的线段AB),经测量在A地的北偏东60°方向,B地的北偏西45°方向的C处有一个以C为圆心,350 m为半径的圆形公园,则修建的这条水渠会不会穿过公园?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=-![]() x+3与x轴相交于点A,与y轴相交于点B,点C是第二象限内任意一点,以点C为圆心的圆与x轴相切于点E,与直线AB相切于点F.
x+3与x轴相交于点A,与y轴相交于点B,点C是第二象限内任意一点,以点C为圆心的圆与x轴相切于点E,与直线AB相切于点F.
(1)如图①,当四边形OBCE是矩形时,求点C的坐标;
(2)如图②,若⊙C与y轴相切于点D,求⊙C的半径r;
(3)在⊙C的移动过程中,能否使△OEF是等边三角形?(只回答“能”或“不能”)

查看答案和解析>>
科目:初中数学 来源: 题型:
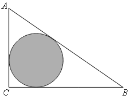
【题目】如图,△ABC是一块绿化带,将阴影部分修建为花圃,已知AB=15,AC=9,BC=12,阴影部分是△ABC的内切圆,一只自由飞翔的小鸟将随机落在这块绿化带上,则小鸟落在花圃上的概率为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
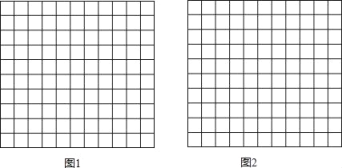
【题目】在所给的11×10方格中,每个小正方形的边长都是1,按要求画出四边形,使它的四个顶点都在小正方形的顶点上.
(1)在图1中画出周长为20的菱形ABCD(非正方形);
(2)在图2中画出邻边比为1:2,面积为40的矩形EFGH,并直接写出矩形EFGH对角线的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com