
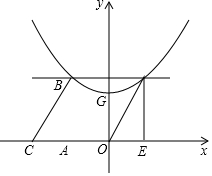
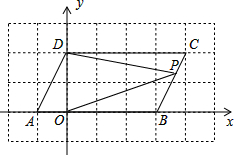
 如图,Rt△ABC中,∠A=90°,∠C=60°,AC在x轴上,点C坐标为(-2,0)抛物线y=ax2+$\frac{2}{3}\sqrt{3}$经过点B,其中△EDO是由△ABC沿x轴向右平移得到,且点D在该抛物线上.已知点G为抛物线的顶点.
如图,Rt△ABC中,∠A=90°,∠C=60°,AC在x轴上,点C坐标为(-2,0)抛物线y=ax2+$\frac{2}{3}\sqrt{3}$经过点B,其中△EDO是由△ABC沿x轴向右平移得到,且点D在该抛物线上.已知点G为抛物线的顶点.分析 (1)如图1中BD与y轴交于点K,由题意四边形OEDK是矩形,四边形OABK也是矩形,TC OE=DK,OA=BK,AC=OE,根据对称性可知BK=DK,推出AC=OA=OE,求出点B坐标,利用待定系数法即可解决问题.
(2)求出直线OB、CD的解析式,解方程组求出点F的坐标,即可判定.
(3)存在.如图2中,由题意Q、P、D、G为顶点的平行四边形时,点P的纵坐标为$\frac{4}{3}$$\sqrt{3}$,当y=$\frac{4}{3}$$\sqrt{3}$时,$\frac{4}{3}$$\sqrt{3}$=$\frac{\sqrt{3}}{3}$x2+$\frac{2}{3}$$\sqrt{3}$,解得x=±$\sqrt{2}$,由此即可解决问题.
解答 解:(1)如图1中,BD与y轴交于点K,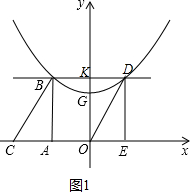
由题意四边形OEDK是矩形,四边形OABK也是矩形,
∴OE=DK,OA=BK,AC=OE,
根据对称性可知BK=DK,
∴AC=OA=OE,
∵C(-2,0),
∴AC=AO=OE=1,
∵∠BCA=60°,
∴BA=$\sqrt{3}$,
∴B(-1,$\sqrt{3}$),
把点B坐标代入y=ax2+$\frac{2\sqrt{3}}{3}$得到$\sqrt{3}$=a+$\frac{2\sqrt{3}}{3}$,
∴a=$\frac{\sqrt{3}}{3}$,
∴抛物线的解析式为y=$\frac{\sqrt{3}}{3}$x2+$\frac{2}{3}$$\sqrt{3}$.
(2)∵B(-1,$\sqrt{3}$),O(0,0),
∴直线OB的解析式为y=-$\sqrt{3}$x,
∵C(-2,0),D(1,$\sqrt{3}$),
∴直线DC的解析式为y=$\frac{\sqrt{3}}{3}$x+$\frac{2\sqrt{3}}{3}$,
由$\left\{\begin{array}{l}{y=\frac{\sqrt{3}}{3}x+\frac{2\sqrt{3}}{3}}\\{y=-\sqrt{3}x}\end{array}\right.$解得$\left\{\begin{array}{l}{x=-\frac{1}{2}}\\{y=\frac{\sqrt{3}}{2}}\end{array}\right.$,
∴点F坐标(-$\frac{1}{2}$,$\frac{\sqrt{3}}{2}$),
对于抛物线y=$\frac{\sqrt{3}}{3}$x2+$\frac{2}{3}$$\sqrt{3}$,
x=-$\frac{1}{2}$时,y=$\frac{3}{4}$$\sqrt{3}$,
∴点F不在抛物线y=$\frac{\sqrt{3}}{3}$x2+$\frac{2}{3}$$\sqrt{3}$上.
(3)存在.如图2中,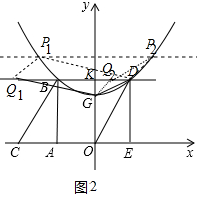
由题意Q、P、D、G为顶点的平行四边形时,点P的纵坐标为$\frac{4}{3}$$\sqrt{3}$,
∴当y=$\frac{4}{3}$$\sqrt{3}$时,$\frac{4}{3}$$\sqrt{3}$=$\frac{\sqrt{3}}{3}$x2+$\frac{2}{3}$$\sqrt{3}$,解得x=±$\sqrt{2}$,
∴点P坐标(-$\sqrt{2}$,$\frac{4}{3}$$\sqrt{3}$)或($\sqrt{2}$,$\frac{4}{3}$$\sqrt{3}$).
点评 本题考查二次函数综合题、一次函数、平行四边形的判定和性质、矩形的性质和判定、平移变换等知识,解题的关键是灵活运用所学知识解决问题,学会构建一次函数,利用方程组求两个函数图象的交点坐标,学会用分类讨论的思想思考问题,属于中考压轴题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
| 星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
| 增减 | +5 | -2 | -4 | +13 | -10 | +16 | -9 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
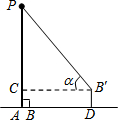 小明利用测角仪和旗杆的拉绳测量学校旗杆的高度.如图,旗杆PA的高度与拉绳PB的长度相等.小明将PB拉到PB'的位置,测得∠PB'C=α=40°(B'C为水平线),测角仪B'D的高度为1米,则旗杆PA的高度表示为( )
小明利用测角仪和旗杆的拉绳测量学校旗杆的高度.如图,旗杆PA的高度与拉绳PB的长度相等.小明将PB拉到PB'的位置,测得∠PB'C=α=40°(B'C为水平线),测角仪B'D的高度为1米,则旗杆PA的高度表示为( )| A. | $\frac{1}{1+cos40°}$ | B. | $\frac{1}{1-cos40°}$ | C. | $\frac{1}{1+sin40°}$ | D. | $\frac{1}{1-sin40°}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在平面直角坐标系中,点A,B的坐标分别为A(a,0),B(b,0),且a,b满足|a+b-2|+$\sqrt{2a-b+5}$=0,现同时将点A,B分别向右平移1个单位,再向上平移2个单位,分别得到点A,B的对应点为C,D.
在平面直角坐标系中,点A,B的坐标分别为A(a,0),B(b,0),且a,b满足|a+b-2|+$\sqrt{2a-b+5}$=0,现同时将点A,B分别向右平移1个单位,再向上平移2个单位,分别得到点A,B的对应点为C,D.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
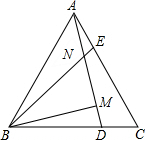 已知:如图:等边△ABC,D、E分别是BC、AC上的点,AD、BE交于N,BM⊥AD于M,若AE=CD,求证:
已知:如图:等边△ABC,D、E分别是BC、AC上的点,AD、BE交于N,BM⊥AD于M,若AE=CD,求证:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,直线y=2x+2与x轴交于点A,与y轴交于点B.
如图,直线y=2x+2与x轴交于点A,与y轴交于点B.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com