Question

1．如图，已知抛物线y=a（x+1）（x-5）与x轴从左至右交于A，B两点，与y轴交于点C（0，5）．
（1）求该抛物线的函数解析式；
（2）D是第一象限内抛物线上的一个动点（与点C，B不重合），过点D作DF⊥x轴于点F，交直线BC于点E，连接BD，CD，直线BC能否把△BDF分成面积之比为2：3的两部分？若能，请求出点D的坐标；若不能，请说明理由．
（3）若M为抛物线对称轴上一动点，△MBC为直角三角形，请直接写出点M的坐标．

Answer 1

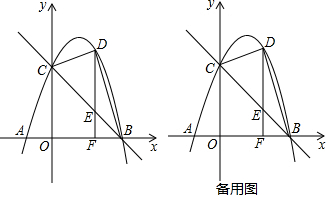
分析 （1）把C点坐标代入y=a（x+1）（x-5）中求出a的值即可得到抛物线解析式；
（2）先解方程-（x+1）（x-5）=0得A（-1，0），B（5，0），再利用待定系数法确定直线BC的解析式为y=-x+5，设D（x，-x²+4x+5），则E（x，-x+5），F（x，0），（0＜x＜5），则DE=-x²+5x，EF=-x+5，利用三角形的面积公式进行讨论：当DE：EF=2：3时，S_△BDE：S_△BEF=2：3；当DE：EF=3：2时，S_△BDE：S_△BEF=3：2，从而可得到关于x的方程，然后解方程求出x就看得到对应的D点坐标；
（3）先确定抛物线的对称轴，如图，设M（2，t），利用两点间的距离公式得到BC²=50，MC²=t²-10t+29，MB²=t²+9，利用勾股定理的逆定理分类讨论：当BC²+MC²=MB²时，△BCM为直角三角形，则50+t²-10t+29=t²+9；当BC²+MB²=MC²时，△BCM为直角三角形，则50+t²+9=t²-10t+29；当MC²+MM²=BC²时，△BCM为直角三角形，则t²-10t+29+t²+9=50，然后分别解关于t的方程，从而可得到满足条件的M点坐标．

解答 解：（1）把C（0，5）代入y=a（x+1）（x-5）得-5a=5，解得a=-1，
所以抛物线解析式为y=-（x+1）（x-5），即y=-x²+4x+5；
（2）能．
当y=0时，-（x+1）（x-5）=0，解得x₁=-1，x₂=5，则A（-1，0），B（5，0），
设直线BC的解析式为y=kx+b，
把C（0，5），B（5，0）代入得$\left\{\begin{array}{l}{b=5}\\{5k+b=0}\end{array}\right.$，解得$\left\{\begin{array}{l}{k=-1}\\{b=5}\end{array}\right.$，
所以直线BC的解析式为y=-x+5，
设D（x，-x²+4x+5），则E（x，-x+5），F（x，0），（0＜x＜5），
∴DE=-x²+4x+5-（-x+5）=-x²+5x，EF=-x+5，
当DE：EF=2：3时，S_△BDE：S_△BEF=2：3，即（-x²+5x）：（-x+5）=2：3，
整理得3x²-17x+10=0，解得x₁=$\frac{2}{3}$，x₂=5（舍去），此时D点坐标为（$\frac{2}{3}$，$\frac{65}{9}$）；
当DE：EF=3：2时，S_△BDE：S_△BEF=3：2，即（-x²+5x）：（-x+5）=3：2，
整理得2x²-13x+15=0，解得x₁=$\frac{3}{2}$，x₂=5（舍去），此时D点坐标为（$\frac{3}{2}$，$\frac{35}{4}$）；
综上所述，当点D的坐标为（$\frac{2}{3}$，$\frac{65}{9}$）或（$\frac{3}{2}$，$\frac{35}{4}$）时，直线BC能否把△BDF分成面积之比为2：3的两部分；
（3）抛物线的对称轴为直线x=2，如图，
设M（2，t），
∵B（5，0），C（0，5），
∴BC²=5²+5²=50，MC²=2²+（t-5）²=t²-10t+29，MB²=（2-5）²+t²=t²+9，
当BC²+MC²=MB²时，△BCM为直角三角形，∠BCM=90°，即50+t²-10t+29=t²+9，解得t=7，此时M点的坐标为（2，7）；
当BC²+MB²=MC²时，△BCM为直角三角形，∠CBM=90°，即50+t²+9=t²-10t+29，解得t=-3，此时M点的坐标为（2，-3）；
当MC²+MM²=BC²时，△BCM为直角三角形，∠CMB=90°，即t²-10t+29+t²+9=50，解得t₁=6，t₂=-1，此时M点的坐标为（2，6）或（2，-1），
综上所述，满足条件的M点的坐标为（2，7），（2，-3），（2，6），（2，-1）．

点评 本题考查了二次函数的综合题：熟练掌握二次函数图象上点的坐标特征和二次函数的性质；会利用待定系数法求直线和抛物线的解析式，会求抛物线与x轴的交点坐标；能运用勾股定理的逆定理判定直角三角形；理解坐标与图形性质，记住两点间的距离公式；学会运用分类讨论的数学思想解决数学问题．