
分析 利用二次根式的乘法法则把$\sqrt{6}$变形为$\sqrt{2}$×$\sqrt{3}$,2变形为$\sqrt{2}$×$\sqrt{2}$,然后用约分即可.
解答 解:原式=$\frac{\sqrt{2}×\sqrt{3}-\sqrt{2}×\sqrt{2}}{\sqrt{2}}$
=$\sqrt{3}$-$\sqrt{2}$.
故答案为$\sqrt{3}$-$\sqrt{2}$.
点评 本题考查了二次根式的混合运算:先把二次根式化为最简二次根式,然后进行二次根式的乘除运算,再合并即可.在二次根式的混合运算中,如能结合题目特点,灵活运用二次根式的性质,选择恰当的解题途径,往往能事半功倍.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:填空题
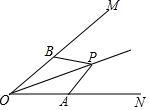 如图,点P在∠MON的平分线上,点A、B在∠MON的两边上,若要使△AOP≌△BOP,那么需要添加一个条件是AO=BO或∠OAP=∠OBP或∠APO=∠BPO(写出一个即可).
如图,点P在∠MON的平分线上,点A、B在∠MON的两边上,若要使△AOP≌△BOP,那么需要添加一个条件是AO=BO或∠OAP=∠OBP或∠APO=∠BPO(写出一个即可).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. |  | B. |  | C. |  | D. |  |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在矩形ABCD中,AB=2,BC=4,点M、N分别在边AD和BC上,沿MN折叠四边形ABCD,使点A、B分别落在A1、B1处,得四边形A1B1NM,其中点B1在DC上,过点M作ME⊥BC于点E,连接BB1,给出下列结论:①∠MNB1=∠ABB1;②△MEN∽△BCB1;③$\frac{MN}{B{B}_{1}}$的值为定值;④当B1C=$\frac{1}{2}$DC时,AM=$\frac{17}{8}$,其中正确结论的序号是①②③.(把所有正确结论的序号都在填在横线上)
如图,在矩形ABCD中,AB=2,BC=4,点M、N分别在边AD和BC上,沿MN折叠四边形ABCD,使点A、B分别落在A1、B1处,得四边形A1B1NM,其中点B1在DC上,过点M作ME⊥BC于点E,连接BB1,给出下列结论:①∠MNB1=∠ABB1;②△MEN∽△BCB1;③$\frac{MN}{B{B}_{1}}$的值为定值;④当B1C=$\frac{1}{2}$DC时,AM=$\frac{17}{8}$,其中正确结论的序号是①②③.(把所有正确结论的序号都在填在横线上)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
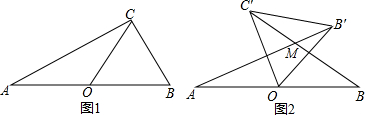
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | k$≤\frac{9}{8}$ | B. | k$>\frac{9}{8}$ | C. | k$≤\frac{9}{8}$且k≠0 | D. | k$<\frac{9}{8}$且k≠0 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com