
分析 根据1与它前面那个数的差的倒数,即an+1=$\frac{1}{1-{a}_{n}}$,即可求得a2;然后根据得到结果出现的规律,即可确定a2012.
解答 解:a1=$-\frac{1}{2}$,
a2=$\frac{1}{1-(-\frac{1}{2})}$=$\frac{2}{3}$,
a3=$\frac{1}{1-\frac{2}{3}}$=3,
a4=$\frac{1}{1-3}$=-$\frac{1}{2}$,
…
-$\frac{1}{2}$,$\frac{2}{3}$,3三个数依次不断循环,
2012÷3=670…2,则a2012=a2=$\frac{2}{3}$.
故答案为:3,$\frac{2}{3}$.
点评 此题考查数字的变化规律,找出数字之间的联系,得出运算规律,利用规律解决问题.


 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
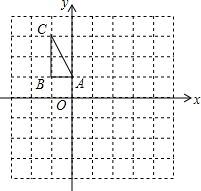 如图,在平面直角坐标系中,△ABC的三个顶点的坐标分别为A(0,1),B(-1,1),C(-1,3).
如图,在平面直角坐标系中,△ABC的三个顶点的坐标分别为A(0,1),B(-1,1),C(-1,3).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
| x | -1 | 0 | 0.5 | 2 |
| y | -1 | 2 | 3.75 | 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com