
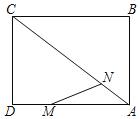
【题目】如图,在矩形ABCD中,AB=6,AD=8,点M,N分别为AD,AC上的动点(不含端点),AN=DM,连结点M与矩形的一个顶点,以该线段为直径作⊙O,当点N和矩形的另一个顶点也在⊙O上时,线段DM的长为_____.
【答案】![]() 或
或![]() .
.
【解析】
分两种情形:如图1中,当点N在CM为直径的圆上时,如图2中,当点N在BM为直径的圆上时,分别利用相似三角形的性质构建方程解决问题即可.
∵四边形ABCD是矩形,
∴∠ADC=90°,AB=CD=6,BC=AD=8,
∴AC=![]() =10,
=10,
如图1中,当点N在CM为直径的圆上时,设DM=AN=x.
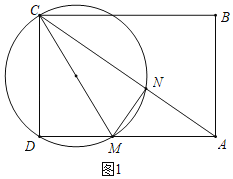
∵CM为直径,
∴∠CNM=90°,
∵∠MAN=∠CAD, ∠ANM=∠ADC=90°,
∴△ANM∽△ADC,
∴![]() ,
,
∴![]() ,
,
解得x=![]() ,
,
∴DM=![]() ;
;
如图2中,当点N在BM为直径的圆上时,设BC与圆的交点为H,连接MH,NH.设DM=AN=y.
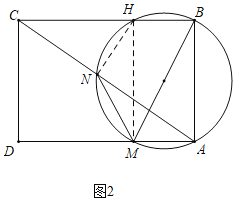
∵BM是直径,
∴∠MHB=90°,
∴∠MHC=∠D=∠DCH=90°,
∴四边形CDMH是矩形,
∴CH=DM=y,
∵∠NCH=∠BCA,∠CHN=∠CAB,
∴△CNH∽△CBA,
∴![]() ,
,
∴![]() ,
,
解得y=![]() ,
,
∴DM=![]() ,
,
故答案为:![]() 或
或![]() .
.


科目:初中数学 来源: 题型:
【题目】小翔在如图1所示的场地上匀速跑步,他从点A出发,沿箭头所示方向经过点B跑到点C,共用时30秒.他的教练选择了一个固定的位置观察小翔的跑步过程.设小翔跑步的时间为t(单位:秒),他与教练的距离为y(单位:米),表示y与t的函数关系的图象大致如图2所示,则这个固定位置可能是图1中的( )

A. 点M B. 点N C. 点P D. 点Q
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市水费采用阶梯收费制度,即:每月用水不超过15吨时,每吨需缴纳水费a元,每月用水量超过15吨时,超过15吨的部分按每吨提高b元缴纳下表是嘉琪家一至四月份用水量和缴纳水费情况.根据表格提供的数据,回答:
月份 | 一 | 二 | 三 | 四 |
月用水量(吨) | 14 | 18 | 16 | 13 |
水费(元) | 42 | 60 | 50 | 39 |
(1)a= 元;b= 元;
(2)求月缴纳水费p(元)与月用水量t(吨)之间的函数关系式;
(3)若嘉琪家五月和六月的月缴水费相差24元,求这两月用水量差的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ABC=90°,以AB为直径作⊙O,点D为⊙O上一点,且CD=CB,连接DO并延长交CB的延长线于点E,连接OC.
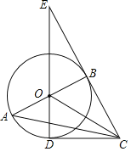
(1) 判断直线CD与⊙O的位置关系,并说明理由;
(2) 若BE=![]() ,DE=3,求⊙O的半径及AC的长.
,DE=3,求⊙O的半径及AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
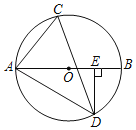
【题目】如图,AB是⊙O的直径,D是⊙O上一点,DE⊥AB于点E,且∠ADE=60°,C是![]() 上一点,连结AC,CD.
上一点,连结AC,CD.
(1)求∠ACD的度数;
(2)证明:AD2=ABAE;
(3)如果AB=8,∠ADC=45°,请你编制一个计算题(不标注新的字母),并直接给出答案.(根据编出的问题层次,给不同的得分)
查看答案和解析>>
科目:初中数学 来源: 题型:
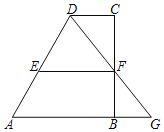
【题目】如图,四边形ABCD中,AB∥CD,CD≠AB,点F在BC上,连DF与AB的延长线交于点G.
(1)求证:CFFG=DFBF;
(2)当点F是BC的中点时,过F作EF∥CD交AD于点E,若AB=12,EF=8,求CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
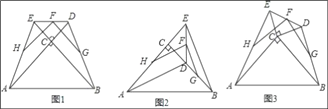
【题目】综合与探究
问题情境:
(1)如图1,两块等腰直角三角板△ABC和△ECD如图所示摆放,其中∠ACB=∠DCE=90°,点F,H,G分别是线段DE,AE,BD的中点,A,C,D和B,C,E分别共线,则FH和FG的数量关系是 ,位置关系是 .
合作探究:
(2)如图2,若将图1中的△DEC绕着点C顺时针旋转至A,C,E在一条直线上,其余条件不变,那么(1)中的结论还成立吗?若成立,请证明,若不成立,请说明理由.
(3)如图3,若将图1中的△DEC绕着点C顺时针旋转一个锐角,那么(1)中的结论是否还成立?若成立,请证明,若不成立,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(问题呈现)阿基米德折弦定理:
如图1,AB和BC是⊙O的两条弦(即折线ABC是圆的一条折弦),BC>AB,点M是![]() 的中点,则从M向BC所作垂线的垂足D是折弦ABC的中点,即CD=DB+BA.下面是运用“截长法”证明CD=DB+BA的部分证明过程.
的中点,则从M向BC所作垂线的垂足D是折弦ABC的中点,即CD=DB+BA.下面是运用“截长法”证明CD=DB+BA的部分证明过程.
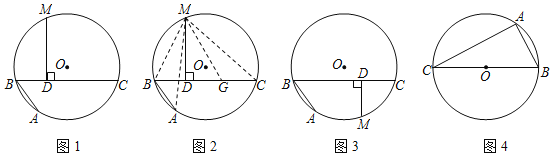
证明:如图2,在CD上截取CG=AB,连接MA、MB、MC和MG.
∵M是![]() 的中点,
的中点,
∴MA=MC①
又∵∠A=∠C②
∴△MAB≌△MCG③
∴MB=MG
又∵MD⊥BC
∴BD=DG
∴AB+BD=CG+DG
即CD=DB+BA
根据证明过程,分别写出下列步骤的理由:
① ,
② ,
③ ;
(理解运用)如图1,AB、BC是⊙O的两条弦,AB=4,BC=6,点M是![]() 的中点,MD⊥BC于点D,则BD= ;
的中点,MD⊥BC于点D,则BD= ;
(变式探究)如图3,若点M是![]() 的中点,(问题呈现)中的其他条件不变,判断CD、DB、BA之间存在怎样的数量关系?并加以证明.
的中点,(问题呈现)中的其他条件不变,判断CD、DB、BA之间存在怎样的数量关系?并加以证明.
(实践应用)根据你对阿基米德折弦定理的理解完成下列问题:
如图4,BC是⊙O的直径,点A圆上一定点,点D圆上一动点,且满足∠DAC=45°,若AB=6,⊙O的半径为5,求AD长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com