
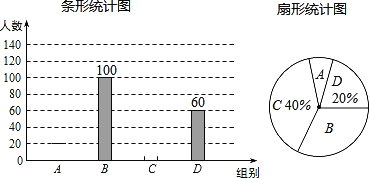
【题目】国家规定,中小学生每天在校体育活动时间不低于1小时,今年受“新冠肺炎”疫情的影响,为落实教育部“停课不停学”的要求,我市中学生进行居家线上学习,为保证广大学生的身心健康,有关部门就“你每天线上学习时在室内或室外安全区域体育锻炼时间是多少”的问题在某校开展了电话调查,随机抽查了部分学生,再根据锻炼时间t(小时)进行分组(A组:t<0.5,B组:0.5≤t<1,C组:1≤t<1.5,D组:t≥1.5),绘制成如图两幅不完整统计图,请根据图中信息回答问题:
(1)此次抽查的学生数为 人,并补全条形统计图;
(2)计算扇形统计图中A组部分所对应的扇形圆心角度数;
(3)若当天该校进行居家线上学习的学生数为1300人,请估计在当天达到国家规定体育活动时间的学生有多少?
【答案】(1)300人,补全图形见解析;(2)24°;(3)780人
【解析】
(1)根据题中两个统计图知,60人的锻炼时间占总的抽样人数20%,即可算出总抽查人数;再算出占抽样40%的C的人数,用抽查的总人数减去B、C、D的人数,即可得A的人数,然后补全条形统计图即可;
(2)用360°乘以A占总抽查人数的比,计算即可;
(3)根据题意知,达标是不低于1小时,C、D两组打标,计算出达标率,再乘以当天该校进行居家线上学习的学生数为1300人,计算即可.
解:(1)60÷20%=300(人).
即此次抽查的学生数为300人.
C组的人数是:300×40%=120(人),
A组的人数是:300﹣100﹣120﹣60=20(人),
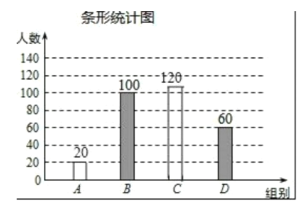
故答案为:300;补全条形统计图如图所示,
(2)图中A组部分所对应的扇形圆心角度数是:360°×![]() =24°;
=24°;
(3)1300×![]() =780(人).
=780(人).
估计在当天达到国家规定体育活动时间的学生有780人.


科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2+bx+c与x轴交于点A(﹣1,0),与y轴的交点在(0,2),(0,3)之间(包含端点),顶点坐标为(1,n),则下列结论:
①2a+b<0;
②﹣1≤a≤﹣![]() ;
;
③对于任意实数m,a(m2﹣1)+b(m﹣1)≤0总成立;
④关于x的方程ax2+bx+c=n+1有两个不相等的实数根.
其中结论正确的序号是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
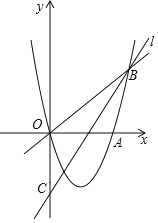
【题目】如图,抛物线y=ax2+bx+c经过O、A(4,0)、B(5,5)三点,直线l交抛物线于点B,交y轴于点C(0,﹣4).点P是抛物线上一个动点.
(1)求抛物线的解析式;
(2)点P关于直线OB的对称点恰好落在直线l上,求点P的坐标;
(3)M是线段OB上的一个动点,过点M作直线MN⊥x轴,交抛物线于点N.当以M、N、B为顶点的三角形与△OBC相似时,直接写出点N的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
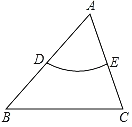
【题目】如图,在△ABC中,D,E分别是△ABC两边的中点,如果![]() (可以是劣弧、优弧或半圆)上的所有点都在△ABC的内部或边上,则称
(可以是劣弧、优弧或半圆)上的所有点都在△ABC的内部或边上,则称![]() 为△ABC的中内弧,例如,图中
为△ABC的中内弧,例如,图中![]() 是△ABC其中的某一条中内弧.若在平面直角坐标系中,已知点F(0,4),O(0,0),H(4,0),在△FOH中,M,N分别是FO,FH的中点,△FOH的中内弧
是△ABC其中的某一条中内弧.若在平面直角坐标系中,已知点F(0,4),O(0,0),H(4,0),在△FOH中,M,N分别是FO,FH的中点,△FOH的中内弧![]() 所在圆的圆心P的纵坐标m的取值范围是_____.
所在圆的圆心P的纵坐标m的取值范围是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,梯形ABCD被分割成两个小梯形①②,和一个小正方形③,去掉③后,①和②可剪拼成一个新的梯形,若EF﹣AD=2,BC﹣EF=1,则AB的长是( )
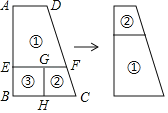
A.6B.3![]() C.9D.3
C.9D.3![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
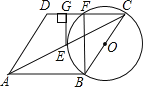
【题目】如图,以ABCD的边BC为直径的⊙O交对角线AC于点E,交CD于点F.连结BF.过点E作EG⊥CD于点G,EG是⊙O的切线.
(1)求证:ABCD是菱形;
(2)已知EG=2,DG=1.求CF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
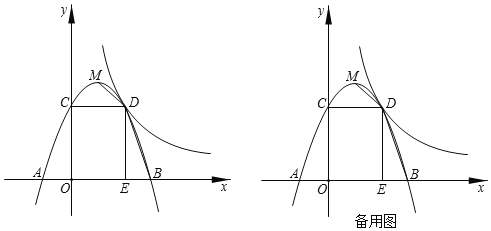
【题目】如图,顶点为M的抛物线y=ax2+bx+3与x轴交于A(﹣1,0),B两点,与y轴交于点C,过点C作CD⊥y轴交抛物线于另一点D,作DE⊥x轴,垂足为点E,双曲线y=![]() (x>0)经过点D,连接MD,BD.
(x>0)经过点D,连接MD,BD.
(1)求抛物线的表达式;
(2)点N,F分别是x轴,y轴上的两点,当以M,D,N,F为顶点的四边形周长最小时,求出点N,F的坐标;
(3)动点P从点O出发,以每秒1个单位长度的速度沿OC方向运动,运动时间为t秒,当t为何值时,∠BPD的度数最大?
查看答案和解析>>
科目:初中数学 来源: 题型:
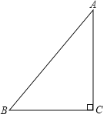
【题目】已知:如图,在Rt△ABC中,∠C=90°,∠A≠∠B.
(1)请利用直尺和圆规作出△ABC关于直线AC对称的△AGC;(不要求写作法,保留作图痕迹)
(2)在AG边上找一点D,使得BD的中点E满足CE=AD.请利用直尺和圆规作出点D和点E;(不要求写作法,保留作图痕迹)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com