
分析 首先根据有理数的乘方的运算方法,求出(-1)2014的值是多少;然后根据零指数幂的运算方法,求出(π-3.14)0的值是多少;最后根据负整数指数幂的运算方法,求出($\frac{1}{2}$)-2的值是多少;再从左向右依次计算,求出算式(-1)2014+(π-3.14)0-($\frac{1}{2}$)-2的值是多少即可.
解答 解:(-1)2014+(π-3.14)0-($\frac{1}{2}$)-2
=1+1-4
=2-4
=-2.
故答案为:-2.
点评 (1)此题主要考查了负整数指数幂的运算,要熟练掌握,解答此题的关键是要明确:①a-p=$\frac{1}{{a}^{p}}$(a≠0,p为正整数);②计算负整数指数幂时,一定要根据负整数指数幂的意义计算;③当底数是分数时,只要把分子、分母颠倒,负指数就可变为正指数.
(2)此题还考查了零指数幂的运算,要熟练掌握,解答此题的关键是要明确:①a0=1(a≠0);②00≠1.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
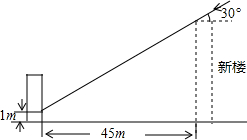 为了解决楼房之间的采光问题,某市有关部门规定:两幢楼房之间的最小距离要使中午12时不能遮光.如图,旧楼的一楼窗台高1m,现计划在旧楼正南方45m处建一幢新楼.已知该市冬天中午12时阳光从正南方照射的光线与水平线的夹角最小为30°,问新楼房最高可建多少米?
为了解决楼房之间的采光问题,某市有关部门规定:两幢楼房之间的最小距离要使中午12时不能遮光.如图,旧楼的一楼窗台高1m,现计划在旧楼正南方45m处建一幢新楼.已知该市冬天中午12时阳光从正南方照射的光线与水平线的夹角最小为30°,问新楼房最高可建多少米?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
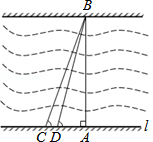 黄冈市为了改善市区交通状况,计划修建一座新大桥.如图,新大桥的两端位于A、B两点,小张为了测量A、B之间的河宽,在垂直于新大桥AB的直线型道路l上测得如下数据:∠BDA=76.1°,∠BCA=68.2°,CD=82米.求AB的长(精确到0.1米).
黄冈市为了改善市区交通状况,计划修建一座新大桥.如图,新大桥的两端位于A、B两点,小张为了测量A、B之间的河宽,在垂直于新大桥AB的直线型道路l上测得如下数据:∠BDA=76.1°,∠BCA=68.2°,CD=82米.求AB的长(精确到0.1米).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com