
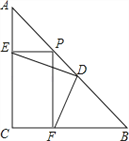
【题目】在△ABC中,∠C=90°,AC=BC=3,D为AB的中点,点P是AB上的一个动点,PE⊥AC于点E,PF⊥BC于点F.
(1)求证:AE=PE;
(2)求证:DE=DF;
(3)连接EF,EF的最小值是多少?
【答案】(1)证明见解析;(2)证明见解析;(3)![]() .
.
【解析】分析:(1)证明△AEP是等腰直角三角形;(2)连接CD,用SAS证明△AED≌△CFD;(3)利用CP=EF,即为求CP的最小值,当CP⊥AB时,CP取最小值.
详解:(1)∵∠C=90°,AC=BC,∴∠CAB=45°.
∵PE⊥AC,∴∠AEP=90°,∴∠APE=90°-45°=45°,
∴∠EAP=∠APE,∴AE=EP.
(2)连接CD,
∵∠C=90°,D为AB的中点,∴CD=AD.
∵AC=BC,∴∠DCF=45°,∴∠A=∠FCD,
∵PE⊥AC,PF⊥BC,∴∠CEP=∠CFP=90°,
∴四边形CEPF是矩形,∴PE=CF,∴AE=CF,
∴△AED≌△CFD(SAS),∴DE=DF.
(3)∵四边形CEPF是矩形,所以EF=CP.
∴EF最小时,CP也最小.
由垂线段最短得,当CP⊥AB时,CP最短,此时,点P与点D重合.
∵△ACP是等腰直角形,∴CP=![]() .
.
则EF的最小值是![]() .
.


科目:初中数学 来源: 题型:
【题目】二次函数中y=ax2+bx﹣3的x、y满足表:
x | … | ﹣1 | 0 | 1 | 2 | 3 | … |
y | … | 0 | ﹣3 | ﹣4 | ﹣3 | m | … |
(1)求该二次函数的解析式;
(2)求m的值并直接写出对称轴及顶点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】嘉淇准备完成题目:化简:![]() ,发现系数“
,发现系数“![]() ”印刷不清楚.
”印刷不清楚.
(1)他把“![]() ”猜成3,请你化简:(3x2+6x+8)–(6x+5x2+2);
”猜成3,请你化简:(3x2+6x+8)–(6x+5x2+2);
(2)他妈妈说:“你猜错了,我看到该题标准答案的结果是常数.”通过计算说明原题中“![]() ”是几?
”是几?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,一次函数y=kx+b的图像分別交x轴、y轴于A、B两点.与反比例函数y=﹣ ![]() 的图像交于C,D两点,DE⊥x轴于点E.已知DE=3,AE=6.
的图像交于C,D两点,DE⊥x轴于点E.已知DE=3,AE=6. 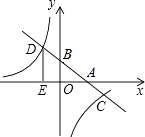
(1)求一次函数的解析式;
(2)直接写出不等式kx+b+ ![]() >0的解集.
>0的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,点E在AD上,连接CE并延长与BA的延长线交于点F,若AE=2ED,CD=3cm,则AF的长为( ) 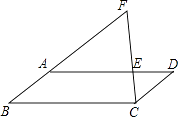
A.5cm
B.6cm
C.7cm
D.8cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图1是一个八角星形纸板,图中有八个直角、八个相等的钝角,每条边都相等,如图2将纸板沿虚线进行切割,无缝隙无重叠的拼成如图3所示的大正方形,其面积为8+4 ![]() ,则图3中线段AB的长为( )
,则图3中线段AB的长为( ) 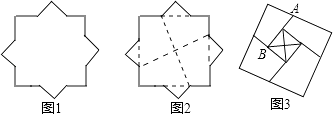
A.![]()
B.2 ![]()
C.![]() ﹣1
﹣1
D.![]() +1
+1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一艘海上巡逻船在A地巡航,这时接到B地海上指挥中心紧急通知:在指挥中心北偏西60°方向的C地有一艘渔船遇险,要求马上前去救援,要求马上前去救援.此时C地位于A地北偏西30°方向上,A地位于B地北偏西75°方向上,A、B两地之间的距离为12海里,则A、C两地之间的距离为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
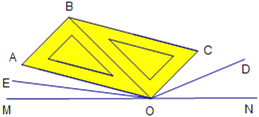
【题目】点O在直线MN上,把两个一样的三角尺按图12所示放置,OD,OE分别平分∠CON和∠AOM.
(1)若∠EOM=10°,求∠NOD的度数;
(2)求∠EOD的度数;
(3)如果保持两个三角尺拼成的图形不变,绕点O转动两个三角尺,使∠CON逐渐变小,那么(2)中的结论会改变吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等腰直角△ABC沿MN所在的直线以2cm/min的速度向右作匀速运动.如果MN=2AC=4cm,那么△ABC和正方形XYMN重叠部分的面积S(cm2)与匀速运动所用时间t(min)之间的函数的大致图像是( )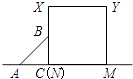
A.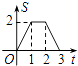
B.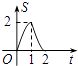
C.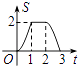
D.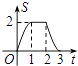
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com