
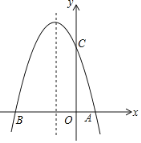
【题目】如图,已知抛物线y=ax2+bx+c(a≠0)的对称轴为x=﹣1,且抛物线经过 A(1,0),C(0,3)两点,与x轴交于点B.
(1)求抛物线的解析式;
(2)在抛物线的对称轴x=﹣1上找一点M,使点M到点A的距离与到点C的距离之和最小,求此时点M的坐标;
(3)设点P为抛物线对称轴x=﹣1上的一个动点,求使△BPC为直角三角形的点P的坐标.
【答案】(1)y=﹣x2﹣2x+3;(2)当点M的坐标为(﹣1,2)时,点M到点A和点C的距离之和最小;(3)P(﹣1,﹣2)或(﹣1,4)或(﹣1,![]()
![]() )或(﹣1,
)或(﹣1,![]() ).
).
【解析】
(1)根据对称轴公式及A、C两点坐标代入即可求出抛物线的解析式;
(2)根据两条线段之和最短时的作图方法找到M即可,然后利用B、C的坐标求出直线BC的解析式,利用BC和对称轴即可求出M的坐标;
(3)设P(﹣1,t),根据平面直角坐标系中任意两点之间的距离公式,即可表示出CB2,PB2和PC2,然后根据直角顶点分类讨论,利用勾股定理求t即可.
解:(1)根据题意得: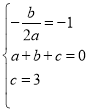 ,解得:
,解得: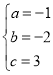 ,
,
∴抛物线的解析式为:y=﹣x2﹣2x+3.
(2)点A的对称点为B,连接BC,直线BC与对称轴x=﹣1的交点为M,则此时AM+MC的值最小.
∵点A与点B关于x=﹣1对称,A(1,0),
∴B(﹣3,0).
设BC的解析式为y=mx+n,将点B和点C的坐标代入得:![]() ,解得:m=1,n=3.
,解得:m=1,n=3.
∴直线BC的解析式为y=x+3.
将x=﹣1代入y=x+3得:y=2,
∴M(﹣1,2).
∴当点M的坐标为(﹣1,2)时,点M到点A和点C的距离之和最小.
(3)设P(﹣1,t).
∵P(﹣1,t),B(﹣3,0),C(0,3),
∴CB2=18,PB2=(﹣1+3)2+t2=t2+4,PC2=(﹣1)2+(t﹣3)2=t2﹣6t+10.
①当点B为直角顶点时,则BC2+PB2=PC2,即18+t2+4=t2﹣6t+10,解得t=﹣2,
∴P(﹣1,﹣2).
②当点C为直角顶点时,BC2+PC2=PB2,即18+t2﹣6t+10=t2+4,解得t=4,
∴P(﹣1,4).
③当点P为直角顶点时,PC2+PB2=BC2,即t2+4+t2﹣6t+10=18,解得:t=![]() 或t=
或t=![]() ,
,
∴P(﹣1,![]() )或(﹣1,
)或(﹣1,![]() ).
).
综上所述,点P的坐标为P(﹣1,﹣2)或(﹣1,4)或(﹣1,![]() )或(﹣1,
)或(﹣1,![]() ).
).


科目:初中数学 来源: 题型:
【题目】已知一次函数![]() 和反比例函数
和反比例函数![]() .
.
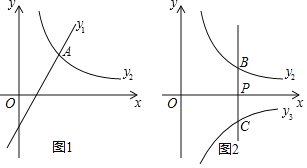
(1)如图1,若![]() ,且函数
,且函数![]() 、
、![]() 的图象都经过点
的图象都经过点![]() .
.
①求![]() ,
,![]() 的值;
的值;
②直接写出当![]() 时
时![]() 的范围;
的范围;
(2)如图2,过点![]() 作
作![]() 轴的平行线
轴的平行线![]() 与函数
与函数![]() 的图象相交于点
的图象相交于点![]() ,与反比例函数
,与反比例函数![]() 的图象相交于点
的图象相交于点![]() .
.
①若![]() ,直线
,直线![]() 与函数
与函数![]() 的图象相交点
的图象相交点![]() .当点
.当点![]() 、
、![]() 、
、![]() 中的一点到另外两点的距离相等时,求
中的一点到另外两点的距离相等时,求![]() 的值;
的值;
②过点![]() 作
作![]() 轴的平行线与函数
轴的平行线与函数![]() 的图象相交于点
的图象相交于点![]() .当
.当![]() 的值取不大于1的任意实数时,点
的值取不大于1的任意实数时,点![]() 、
、![]() 间的距离与点
间的距离与点![]() 、
、![]() 间的距离之和
间的距离之和![]() 始终是一个定值.求此时
始终是一个定值.求此时![]() 的值及定值
的值及定值![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
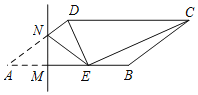
【题目】如图,已知ABCD中,AB=16,AD=10,sinA=![]() ,点M为AB边上一动点,过点M作MN⊥AB,交AD边于点N,将∠A沿直线MN翻折,点A落在线段AB上的点E处,当△CDE为直角三角形时,AM的长为_____.
,点M为AB边上一动点,过点M作MN⊥AB,交AD边于点N,将∠A沿直线MN翻折,点A落在线段AB上的点E处,当△CDE为直角三角形时,AM的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
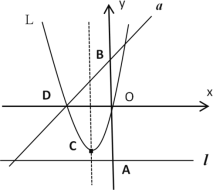
【题目】如图,若m是正数,直线l:y=-m与y轴交于点A;直线a:y=x+m与y轴交于点B;抛物线L:y= x2+mx的顶点为C,且L与x轴左交点为D.
(1)若AB=12,求m的值,此时在抛物线的对称轴上存在一点P使得△![]() 的周长最小,求点P坐标;
的周长最小,求点P坐标;
(2)当点C在直线l上方时,求点C与直线l距离的最大值;
(3)在抛物线L和直线a所围成的封闭图形的边界上,把横、纵坐标都是整数的点称为“美点”,分别直接写出m=2020和m=2020.5时“美点”的个数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】玛丽和冯刚做一种游戏,在一个不透明的布袋里装有4个大小、质地均相同小球,球上分别标有数字1、2、3、4,随机从布袋中摸出一个小球,记下数字后放回布袋里,再随机从布袋中摸出一个小球,若这两个小球上的数字之和能被2整除的概率大则玛丽赢;若两个小球上的数字之和能被3整除的概率大则冯刚赢。这个游戏双方公平吗?请列表格或画树状图说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】东东玩具商店用500元购进一批悠悠球,很受中小学生欢迎,悠悠球很快售完,接着又用900元购进第二批这种悠悠球,所购数量是第一批数量的1.5倍,但每套进价多了5元.
(1)求第一批悠悠球每套的进价是多少元;
(2)如果这两批悠悠球每套售价相同,且全部售完后总利润不低于25%,那么每套悠悠球的售价至少是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
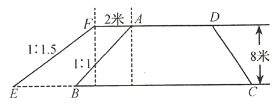
【题目】如图,沿水库拦水坝的背水坡将坝顶加宽2米,坡度由原来的![]() 改为
改为![]() .已知坝高8米,坝长为60米.
.已知坝高8米,坝长为60米.
求:(1)加宽部分横断面![]() 的面积;
的面积;
(2)完成这一工程需要多少立方米土?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线y=﹣![]() 与x轴交于A、B两点(点A在点B左侧),与y轴交于点C.
与x轴交于A、B两点(点A在点B左侧),与y轴交于点C.
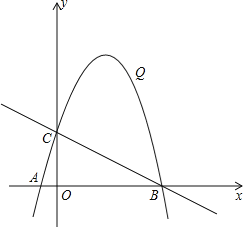
(1)求出△ABC的周长.
(2)在直线BC上方有一点Q,连接QC、QB,当△QBC面积最大时,一动点P从Q出发,沿适当路径到达y轴上的M点,再沿与对称轴垂直的方向到达对称轴上的N点,连接BN,求QM+MN+BN的最小值.
(3)在直线BC上找点G,K是平面内一点,在平面内是否存在点G,使以O、C、G、K为顶点的四边形是菱形?若存在,求出K的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com