
分析 (1)根据中位数和众数的定义可以解答本题;
(2)根据平均数和方差的计算方法可以解答本题;
(3)根据方差越小越稳定可以解答本题.
解答 解:(1)甲运动员的成绩按照从小到大排列是:6、7、8、8、9,
∴甲运动员这5次选拔赛成绩的中位数和众数分别是8,8;
(2)由题意可得,
$\overline{{x}_{乙}}$=$\frac{9+7+5+8+6}{5}$=7,
${{s}^{2}}_{乙}=\frac{(9-7)^{2}+(7-7)^{2}+(5-7)^{2}+(8-7)^{2}+(6-7)^{2}}{5}$=2;
(3)∵甲的方差是1.04,乙的方差是2,1.04<2,
∴应该选择甲运动员参加比赛.
点评 本题考查平均数、方差、中位数、众数,解答本题的关键是明确平均数和方差的计算方法、知道什么是中位数和众数.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
| A. | k>-3 | B. | k<5 | C. | k>-3且k≠1 | D. | k<5且k≠1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
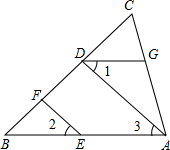 请完成下面的证明过程:
请完成下面的证明过程:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com