
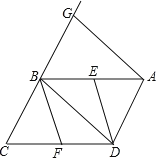
【题目】已知:如图,在平行四边形![]() 中,
中,![]() 分别为边
分别为边![]() 的中点,连接
的中点,连接![]() ,作
,作![]() 交
交![]() 的延长线于
的延长线于![]() .
.
(1)求证:![]() ;
;
(2)若四边形![]() 是矩形,则四边形
是矩形,则四边形![]() 是什么特殊四边形?证明你的结论.
是什么特殊四边形?证明你的结论.
【答案】(1)证明见解析;(2)当四边形![]() 是矩形时,四边形
是矩形时,四边形![]() 是菱形,证明见解析.
是菱形,证明见解析.
【解析】
(1)先根据平行四边形的性质得出![]() ,再根据线段的中点定义、等量代换得出
,再根据线段的中点定义、等量代换得出![]() ,然后根据三角形全等的判定定理即可得证;
,然后根据三角形全等的判定定理即可得证;
(2)先根据平行四边形的性质、线段中点的定义得出![]() ,
,![]() ,再根据平行四边形的判定可得四边形
,再根据平行四边形的判定可得四边形![]() 是平行四边形,然后根据矩形的性质、直角三角形的中线性质得出
是平行四边形,然后根据矩形的性质、直角三角形的中线性质得出![]() ,且
,且![]() 与
与![]() 不垂直,由此可得平行四边形
不垂直,由此可得平行四边形![]() 是菱形.
是菱形.
(1)证明:∵四边形![]() 是平行四边形
是平行四边形
![]()
∵点![]() 分别是
分别是![]() 的中点
的中点
![]()
![]()
在![]() 和
和![]() 中,
中,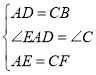
∴![]() ;
;
(2)当四边形![]() 是矩形时,四边形
是矩形时,四边形![]() 是菱形.证明过程如下:
是菱形.证明过程如下:
![]() 四边形
四边形![]() 是平行四边形
是平行四边形
![]() ,
,![]()
∵点![]() 分别是
分别是![]() 的中点
的中点
∴![]()
![]()
∴四边形![]() 是平行四边形
是平行四边形
∵四边形![]() 是矩形
是矩形
![]()
![]() 是直角三角形,不是等腰直角三角形
是直角三角形,不是等腰直角三角形
∵点![]() 是
是![]() 的中点
的中点
![]() ,且
,且![]() 与
与![]() 不垂直
不垂直
∴平行四边形![]() 是菱形,不是正方形
是菱形,不是正方形
故当四边形![]() 是矩形时,四边形
是矩形时,四边形![]() 是菱形.
是菱形.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,AB=3cm,以B为圆心,1cm长为半径画⊙B,点P在⊙B上移动,连接AP,并将AP绕点A逆时针旋转90°至AP′,连接BP′.在点P移动的过程中,BP′长度的最小值为_____cm.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于三角函数有如下的公式:
sin(α+β)=sinαcosβ+cosαsinβ①
cos(α+β)=cosαcosβ﹣sinαsinβ②
tan(α+β)=![]() ③
③
利用这些公式可将某些不是特殊角的三角函数转化为特殊角的三角函数来求值,如:
tan105°=tan(45°+60°)=![]() =﹣(2+
=﹣(2+![]() ).
).
根据上面的知识,你可以选择适当的公式解决下面的实际问题:
如图,直升飞机在一建筑物CD上方A点处测得建筑物顶端D点的俯角α=60°,底端C点的俯角β=75°,此时直升飞机与建筑物CD的水平距离BC为42m,求建筑物CD的高.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A. “任意画一个三角形,其内角和为![]() ”是随机事件;
”是随机事件;
B. 某种彩票的中奖率是![]() ,说明每买100张彩票,一定有1张中奖;
,说明每买100张彩票,一定有1张中奖;
C. “篮球队员在罚球线上投篮一次,投中”为随机事件;
D. 投掷一枚质地均匀的硬币100次,正面向上的次数一定是50次.
查看答案和解析>>
科目:初中数学 来源: 题型:
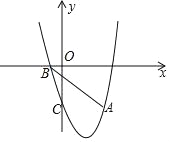
【题目】如图,抛物线y=ax2+bx+c经过点A(2,﹣3),且与x轴交点坐标为(﹣1,0),(3,0)
(1)求抛物线的解析式;
(2)在直线AB下方抛物线上找一点D,求出使得△ABD面积最大时点D的坐标;
(3)点M在抛物线上,点N在抛物线的对称轴上,是否存在以点A,B,M,N为顶点的四边形是平行四边形?若存在,直接写出所有符合条件的点M的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面的解题过程,解答后面的问题:
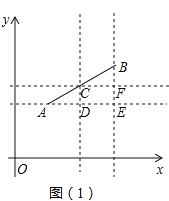
如图![]() ,在平面直角坐标系
,在平面直角坐标系![]() 中,
中,![]() ,
,![]() ,
,![]() 为线段
为线段![]() 的中点,求
的中点,求![]() 点的坐标;
点的坐标;
解:分别过![]() ,
,![]() 做
做![]() 轴的平行线,过
轴的平行线,过![]() ,
,![]() 做
做![]() 轴的平行线,两组平行线的交点如图
轴的平行线,两组平行线的交点如图![]() 所示,设
所示,设![]() ,则
,则![]() ,
,![]() ,
,![]()
由图![]() 可知:
可知:
![]()
![]()
![]() 线段
线段![]() 的中点
的中点![]() 的坐标为
的坐标为![]()
(应用新知)
利用你阅读获得的新知解答下面的问题:
(1)已知![]() ,
,![]() ,则线段
,则线段![]() 的中点坐标为
的中点坐标为
(2)平行四边形![]() 中,点
中,点![]() ,
,![]() ,
,![]() 的坐标分别为
的坐标分别为![]() ,
,![]() ,
,![]() ,利用中点坐标公式求点
,利用中点坐标公式求点![]() 的坐标。
的坐标。
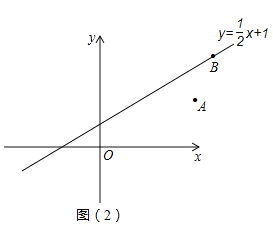
(3)如图![]() ,点
,点![]() 在函数
在函数![]() 的图象上,
的图象上, ![]() ,
,![]() 在
在![]() 轴上,
轴上,![]() 在函数
在函数![]() 的图象上 ,以
的图象上 ,以![]() ,
,![]() ,
,![]() ,
,![]() 四个点为顶点,且以
四个点为顶点,且以![]() 为一边构成平行四边形,直接写出所有满足条件的
为一边构成平行四边形,直接写出所有满足条件的![]() 点坐标。
点坐标。
查看答案和解析>>
科目:初中数学 来源: 题型:
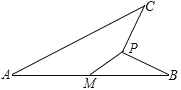
【题目】如图,线段 AB=4,M 为 AB 的中点,动点 P 到点 M 的距离是 1,连接 PB,线段
PB 绕点 P 逆时针旋转 90°得到线段 PC,连接 AC,则线段 AC 长度的最大值是_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
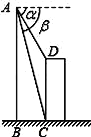
【题目】如图,AB、CD为两个建筑物,建筑物AB的高度为60米,从建筑物AB的顶点A点测得建筑物CD的顶点C点的俯角∠EAC为30°,测得建筑物CD的底部D点的俯角∠EAD为45°.
(1)求两建筑物底部之间水平距离BD的长度;
(2)求建筑物CD的高度(结果保留根号).
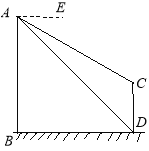
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若一组数据a,b,c的平均数为5,方差为4,那么数据a+2,b+2,c+2的平均数和方差分别是( )
A.5,4B.4,5C.7,4D.7,3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com