
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
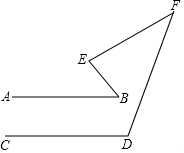 已知,如图,∠E=80°,且$\sqrt{∠B-n-20°}$+(∠D-80°-n)2+|∠F-40°|=0.(n为常数,且0°<n<100°).
已知,如图,∠E=80°,且$\sqrt{∠B-n-20°}$+(∠D-80°-n)2+|∠F-40°|=0.(n为常数,且0°<n<100°).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
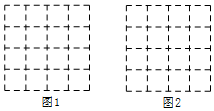 如图,正方形网格中的每个小正方形的边长都是1,每个小格的顶点叫做格点.
如图,正方形网格中的每个小正方形的边长都是1,每个小格的顶点叫做格点.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
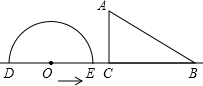 如图,半圆O直径DE=12,Rt△ABC中,BC=12,∠ACB=90°,∠ABC=30°.半圆O从左到右运动,在运动过程中,点D,E始终在直线BC上,半圆O在△ABC的左侧,当△ABC的一边与半圆O所在的圆相切时,如果半圆O与直径DE围成的区域与△ABC的三边围成的区域有重叠部分,重叠部分的面积为9π或9$\sqrt{3}$+6π.
如图,半圆O直径DE=12,Rt△ABC中,BC=12,∠ACB=90°,∠ABC=30°.半圆O从左到右运动,在运动过程中,点D,E始终在直线BC上,半圆O在△ABC的左侧,当△ABC的一边与半圆O所在的圆相切时,如果半圆O与直径DE围成的区域与△ABC的三边围成的区域有重叠部分,重叠部分的面积为9π或9$\sqrt{3}$+6π.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
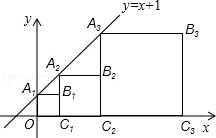 正方形A1B1C1O,A2B2C2C1,A3B3C3C2,…按如图的方式放置,点A1,A2,A3…和点C1,C2,C3…分别在直线y=x+1和x轴上,则点Bn的坐标为(2n-1,2n-1).
正方形A1B1C1O,A2B2C2C1,A3B3C3C2,…按如图的方式放置,点A1,A2,A3…和点C1,C2,C3…分别在直线y=x+1和x轴上,则点Bn的坐标为(2n-1,2n-1).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
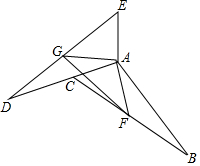 如图,把△ABC绕点A顺时针旋转n度(0<n<180)后得到△ADE,并使点D落在AC的延长线上.
如图,把△ABC绕点A顺时针旋转n度(0<n<180)后得到△ADE,并使点D落在AC的延长线上.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com