练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    (1)任选以下三个条件中的一个，求二次函数的解析式；

      

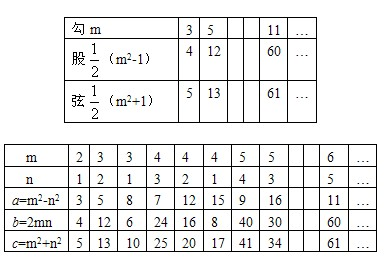
      ①y随x变化的部分数值规律如下表：

    x

    -1

    0

    1

    2

    3

    y

    0

    3

    4

    3

    0

     ②有序数对、、满足；

      ③已知函数的图象的一部分（如图）．

     (2)直接写出二次函数的三个性质．

    解析：（1）

          方法一：由可得：C=3，，，所以，，C=3，

           所以二次函数解析式为：

          方法二：由②可得：，，，

           解之得：，，C=3，

           所以二次函数解析式为：

           方法三：由③可得：C=3，，，解之得：，，C=3，

           所以二次函数解析式为：

          （三种选其一即可）

         （2）1、对称轴为，

              2、开口向下

              3、与轴有2个交点

              4、交  轴正半轴

       考察知识：待定系数法求二次函数解析式、二次函数的性质及图像

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：阅读理解

    阅读材料并解答问题：
    我国是最早了解和应用勾股定理的国家之一，古代印度、希腊、阿拉伯等许多国家也都很重视对勾股定理的研究和应用，古希腊数学家毕达哥拉斯首先证明了勾股定理，在西方，勾股定理又称为“毕达哥拉斯定理”．
    关于勾股定理的研究还有一个很重要的内容是勾股数组，在《几何》课本中我们已经了解到，“能够成为直角三角形三条边的三个正整数称为勾股数”，以下是毕达哥拉斯等学派研究出的确定勾股数组的两种方法：
    方法1：若m为奇数（m≥3），则a=m，b=
    1
    2
    （m2-1）和c=
    1
    2
    （m2+1）是勾股数．
    方法2：若任取两个正整数m和n（m＞n），则a=m2-n2，b=2mn，c=m2+n2是勾股数．
    （1）在以上两种方法中任选一种，证明以a，b，c为边长的△ABC是直角三角形；
    （2）请根据方法1和方法2按规律填写下列表格：
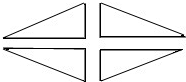
    精英家教网
    （3）某园林管理处要在一块绿地上植树，使之构成如下图所示的图案景观，该图案由四个全等的直角三角形组成，要求每个三角形顶点处都植一棵树，各边上相邻两棵树之间的距离均为1米，如果每个三角形最短边上都植6棵树，且每个三角形的各边长之比为5：12：13，那么这四个直角三角形的边长共需植树
     
    棵．
    精英家教网

    查看答案和解析>>

    科目：初中数学 来源： 题型：

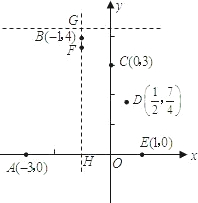    在平面直角坐标系中给定以下五个点A（-3，0），B（-1，4），C（0，3），D（
    1
    2
    ，
    7
    4
    ），E（1，0）．
    （1）请从五点中任选三点，求一条以平行于y轴的直线为对称轴的抛物线的解析式；
    （2）求该抛物线的顶点坐标和对称轴，并画出草图．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    精英家教网在平面直角坐标系中给定以下五个点A（-3，0），B（-1，4），C（0，3），D（
    1
    2
    ，
    7
    4
    ），E（1，0）．
    （1）请从五点中任选三点，求一条以平行于y轴的直线为对称轴的抛物线的解析式；
    （2）求该抛物线的顶点坐标和对称轴，并画出草图；
    （3）已知点F（-1，
    15
    4
    ）在抛物线的对称轴上，直线y=
    17
    4
    过点G（-1，
    17
    4
    ）且垂直于对称轴．验证：以E（1，0）为圆心，EF为半径的圆与直线y=
    17
    4
    相切．请你进一步验证，以抛物线上的点D（
    1
    2
    ，
    7
    4
    ）为圆心DF为半径的圆也与直线y=
    17
    4
    相切．由此你能猜想到怎样的结论．

    查看答案和解析>>

    科目：初中数学 来源：第2章《二次函数》中考题集（36）：2.7 最大面积是多少（解析版） 题型：解答题

    在平面直角坐标系中给定以下五个点A（-3，0），B（-1，4），C（0，3），D（，），E（1，0）．
    （1）请从五点中任选三点，求一条以平行于y轴的直线为对称轴的抛物线的解析式；
    （2）求该抛物线的顶点坐标和对称轴，并画出草图；
    （3）已知点F（-1，）在抛物线的对称轴上，直线y=过点G（-1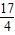，）且垂直于对称轴．验证：以E（1，0）为圆心，EF为半径的圆与直线y=相切．请你进一步验证，以抛物线上的点D（，）为圆心DF为半径的圆也与直线y=相切．由此你能猜想到怎样的结论．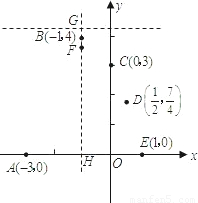

    查看答案和解析>>

    科目：初中数学 来源：第2章《二次函数》中考题集（37）：2.4 二次函数的应用（解析版） 题型：解答题

    在平面直角坐标系中给定以下五个点A（-3，0），B（-1，4），C（0，3），D（，），E（1，0）．
    （1）请从五点中任选三点，求一条以平行于y轴的直线为对称轴的抛物线的解析式；
    （2）求该抛物线的顶点坐标和对称轴，并画出草图；
    （3）已知点F（-1，）在抛物线的对称轴上，直线y=过点G（-1，）且垂直于对称轴．验证：以E（1，0）为圆心，EF为半径的圆与直线y=相切．请你进一步验证，以抛物线上的点D（，）为圆心DF为半径的圆也与直线y=相切．由此你能猜想到怎样的结论．

    查看答案和解析>>

    同步练习册答案